암호 뉴비들의 암호 깨는 대회 출전기

작년과 마찬가지로, 2021년 암호분석경진대회에 참가하였고, 우수상을 수상하였다.

정작 시상식은 중간고사하고 겹쳐서 못갔다.

혼자서 나간 작년 대회와는 달리, 이번에는 고3이기 때문에 시간이 없고^[1], 수상자에 대해 동일 팀 구성을 제한했기 때문에 11기 정진용 학생과 같이 "Team Crypt0newbies"라는 팀명으로 대회에 참가했다.

대회 총평

작년 대회에서 수상하긴 했지만, 우리가 암호에 대해 거의 아무것도 모르는 "뉴비" 상태임은 변함이 없다. 작년과 마찬가지로 문제를 해결하기 위해 논문과 책을 읽고, 직접 코드를 작성하는 과정을 거쳤다. 2020년 대회와 비교해서 난이도는 비슷하다는 느낌이 들었다.^[2] 하지만 작년에 비해 문제에서 크고 작은 오류와 빠진 조건이 많이 있었고, 이 때문에 문제 해결에 어려움을 겪었다.

문제가 궁금하다면, 대회 사이트에서 다운로드하면 된다.

1번: 고전 암호 문제

1번 문제는 사실 가장 마지막에 푼 문제이고, 여기서 설명하는 것이 정답이라는 확신이 없다.

민준이는 세계 여행을 계획하고 다음과 같은 순서로 세계 12개국을 방문하기로 하였다.

방글라데시 – 부탄 – 러시아 – 벨로루시 – 스위스 – 스페인 – 이탈리아 – 사우디아라비아 – 터키 – 태국– 과테말라 – 미국

이 여정에는 단어가 숨겨져 있다. 숨겨진 단어를 찾고 그 근거를 제시하시오.

1번 문제를 보자마자, 우리는 아무 생각이 나지 않았다. 지도는 왜 준거지? 벨라루스를 왜 굳이 벨로루시라고 준 거지? 등등 의문이 생겼다. 가장 먼저 생각해 본 것은 나라 이름들이었다. 한글을 그대로 암호로 만들 것 같지는 않고^[3], 무언가 암호를 만들기 쉬운 숫자나, 영문으로 변환해야 한다는 생각이 들었다. 그런데 영문으로 변환한다면 상당히 모호해진다. 미국은 "USA", "United States", "United States of America" 중에 어떤 것으로 바궈야 할까? 그런 이유로 국가들을 숫자로 나타내야 하지 않을까 하는 생각을 하게 되었고, 국가 코드를 사용해야겠다는 생각을 했다.

문제를 해결하기 위해 ISO 3166-1 국가 코드로 각 여행지들을 숫자로 나타냈다.

country = [50, 64, 643, 112, 756, 724, 380, 682, 792, 764, 320, 840]

이 숫자들에 대해 26으로 나눈 나머지를 취하고, 0부터 25까지 각 숫자에 알파벳 하나씩 대응될 것이라는 생각을 했다. 이러한 퍼즐을 cryptogram이라고 하는데, 이를 해결하기 위해 cryptogram solver를 사용하여 bristlegrass^[4]라는 답을 얻었다.

2번: 경량 암호 PRINCE에 대한 공격

이 문제는 4라운드 PRINCE를 이용해 암호화한 평문-암호문 쌍이 주어졌을 때, 암호화 키를 찾는 문제였다. PRINCE 암호는 하드웨어 구현을 용이하게 하기 위해 설계된 암호이다. 하드웨어에서 구현했을 때, 한 사이클 내에 암호화 결과가 나오면서도, 칩의 die size를 최소화하도록 한 것이다.

PRINCE 암호는 64비트 블록을 128비트 키로 암호화하는 블록 암호이다. PRINCE 암호는 FX 구성에 기반하여, 128비트짜리 키 \(k\)를 다음과 같이 64비트짜리 조각 2개로 나누고^[5]

\[k=k_0\|k_1\]

다음과 같은 사상으로 192비트로 키를 확장한다.^[6]

\[(k_0\|k_1)\to (k_0\|k_0'\|k_1) := (k_0\|(k_0\ggg 1)\oplus(k_0\gg 63)\|k_1)\]

이 사상을 통해 나온 \(k_0, k_0', k_1\)은 모두 암호화 과정에서 사용되는 64비트 키들이다. 이 키들을 이용해 암호화되는 과정은 다음 그림과 같다. 각 라운드에서 라운드 상수 \(RC_n\)와 \(k_1\)을 XOR하고, S-layer와 M-layer를 지나가는 것을 볼 수 있다.^[7]

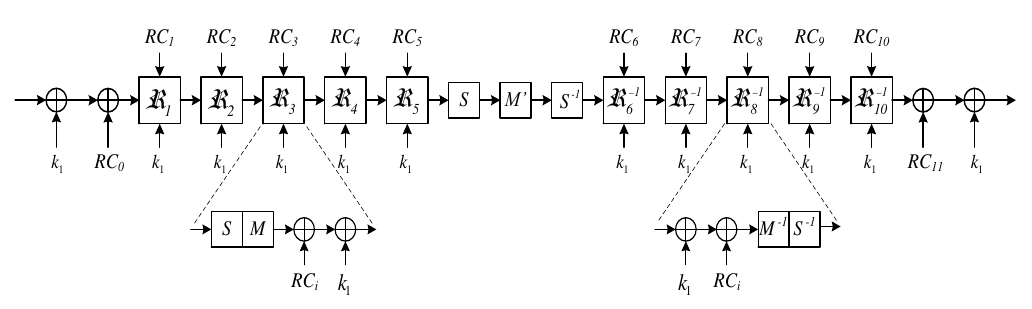
PRINCE 암호에 대한 공격을 찾던 중, PRINCE 암호 연구팀에서 챌린지를 진행한 것을 알게 되었다. 챌린지는 PRINCE 암호에서 라운드 수를 줄이거나, 키 화이트닝을 제거한 '쉬워진' PRINCE 암호를 분석하는 것이었고, 4라운드 PRINCE에 대한 연구도 찾을 수 있었다. 이 문제를 풀기 위해서 "Practical Attacks on the Round-reduced PRINCE"라는 논문을 참조했다.

논문에서는 integral cryptanalysis라는 기법으로 4라운드 PRINCE를 공격한다. Integral cryptanalysis는 differential cryptanalysis라는 유명한 분석 기법과 관련이 있다.^[8] Differential cryptanalysis는 여러 개의 평문의 차이를 알고 있을 때 암호문끼리의 차이를 보고 분석하는 미분의 성격이 강하다면, integral cryptanalysis는 합^[9]을 알고 있는 암호문들을 모두 암호화해서 암호문들의 합을 보고 분석하는 적분의 성격이 강하다. 마침 문제에서 준 평문들을 보면, 어떤 문자열에 대해 한 비트씩만 바꾼 조합들이 들어 있었다.

09 23 be 84 e1 6c d6 ae
19 23 be 84 e1 6c d6 ae
29 23 be 84 e1 6c d6 ae
39 23 be 84 e1 6c d6 ae
49 23 be 84 e1 6c d6 ae
59 23 be 84 e1 6c d6 ae
69 23 be 84 e1 6c d6 ae
79 23 be 84 e1 6c d6 ae
89 23 be 84 e1 6c d6 ae
99 23 be 84 e1 6c d6 ae
a9 23 be 84 e1 6c d6 ae
b9 23 be 84 e1 6c d6 ae
c9 23 be 84 e1 6c d6 ae
d9 23 be 84 e1 6c d6 ae
e9 23 be 84 e1 6c d6 ae
f9 23 be 84 e1 6c d6 ae
20 23 be 84 e1 6c d6 ae
21 23 be 84 e1 6c d6 ae

문제에서 주어진 평문의 일부를 16진수로 나타내면 위와 같다. 29 23 be 84 e1 6c d6 ae라는 문자열에서 첫 4비트를 바꾼 모든 경우의 수가 나와 있다.^[10] 그 다음에는 첫 5~8번째 비트를 바꾸는 모든 경우의 수가 있고, 9~12번째...로 마지막 4비트까지 계속 이어진다. 이렇게 비트가 바뀌는 4비트짜리 구간을 active nibble이라고 하고, integral cryptanalysis는 이 active nibble에 주목한다. 앞서 소개한 논문에서는 4라운드 중 마지막 라운드에 주목했다. 마지막 라운드와 마지막 라운드 이후 화이트닝 단계에서는 \(RC_3, k_1, k_0'\)을 XOR한다. 그런데, 어떤 암호문에 대해서든 XOR하기 전까지 부분적으로 암호화된 데이터에 대해서, active nibble이 한 개 있을 때에는 16가지 경우의 평문을 입력한 결과를 XOR하면 0이 나온다. 이 성질을 이용해 역으로 \(k_0'\oplus k_1\)의 값을 구할 수 있고, 이진수로 나타내면 다음과 같다.

1100000101011010010010111100100001010101010101010100100001001011

논문에서는 더 나아가 active nibble이 4개 있는 평문들을 이용해 전체 키를 복구했지만, 제시된 데이터로는 그것이 불가능했고, brute force가 필요해졌다. 가장 무식하게 공격한다면 128비트를 모두 찍어야 하기 때문에 \(2^{128}\)개의 키를 확인해봐야 한다. 당연히 이것은 불가능하다.^[11] 조금만 생각해보면 확인할 키의 개수를 \(2^{64}\)로 줄일 수 있다. \(k_0'\oplus k_1\)의 값을 알고 있기 때문에, \(k_0\)이나 \(k_1\)의 값은 XOR 한번으로 계산 가능하기 때문이다. 하지만 \(2^{64}\)개의 키도 너무 많다.

탐색 공간을 더욱 줄이기 위해, 문제의 조건에서 힌트를 얻을 수 있다. 문제에서는 암호화 키가 알파벳 소문자로만 이루어져 있다고 명시되어 있다. 'a'의 아스키 코드값은 97이고, 'z'의 아스키 코드값은 122이다. 이를 이진수로 나타내면 01100001과 01111010인데, 첫 3비트가 같음을 알 수 있다. 그런데 이미 \(k_0'\oplus k_1\)의 값을 알고 있고, \(k_0'=(k_0\ggg 1)\oplus(k_0\gg 63)\)이기 때문에 \(k_0\gg 63=0\)이고, \(k_0'=k_0\ggg 1\)이다. 이를 이용해 \(k_0'\)과 \(k_1\)의 일부 비트를 복구할 수 있다. 이 방법으로 알 수 없는 비트는 X로 표시했다.

k0' = 1011XXXX0011XXXX0011XXXX1011XXXX0011XXXX0011XXXX0011XXXX0011XXXX
k1  = 0111XXXX0110XXXX0111XXXX0111XXXX0110XXXX0110XXXX0111XXXX0111XXXX

이제 \(k_1\)의 남은 32비트를 탐색하여 키를 재구성하고, 재구성한 키로 주어진 평문을 암호화할때 결과가 맞는지를 체크하면 hzqzzlpsugsuhcpr라는 키를 얻는다.

3번: ECDSA 구현하기

3번은 스택 프로세서를 구현하라는 문제이다. 문제에서는 프로세서라고 나와 있었지만 우리가 구현한 것은 간단한 언어의 인터프리터에 가까웠다. 우리가 구현할 프로세서(인터프리터)는 비트코인의 P2PKH 트랜잭션 과정^[12]과 비슷한 프로토콜로 ECDSA 서명을 생성, 검증할 수 있어야 했다.

ECDSA는 간단히 말하면, 타원 곡선 기반의 공개키 암호로 디지털 서명을 생성한다. 타원 곡선이라는 이름을 듣고, 고등학교 기하 시간에 배우는 "찌그러진 원"이라는 의미의 타원을 생각할지도 모른다. 하지만 타원 곡선은 전혀 타원처럼 생기지 않았다.

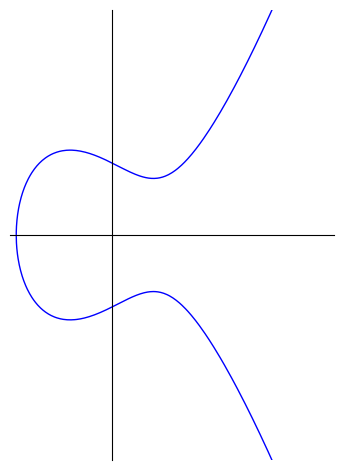
타원 곡선이 저렇게 생긴 것은 그렇다치고, 곡선으로 암호를 만든다는 사실도 비현실적으로 들린다. 주로 이산수학, 정수론과 관련 있는 암호가, 기하학적인 곡선과 무슨 관련이 있는지 상상하기 쉽지 않다. 당연히 타원곡선 그 자체를 가지고는 암호를 만들수 없고, 곡선을 유한체에 제한한다. 위 그림을 유한체 \(\mathbb{F}_{101}\)에 제한하여 그래프를 그리면 다음과 같다.^[13]

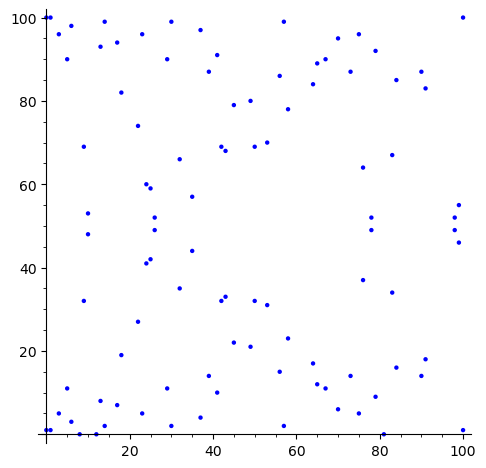
이걸 곡선이라고 불러야 할지도 의문이다. 이제 셀수 없이 많았던 점들이 없어지고, 100개의 점들만 남았다. 이들 점에 대해서, 덧셈 연산을 정의한다. 타원 곡선의 점 \((x_1, y_1), (x_2, y_2)\)를 더한 결과 \((x_3, y_3)\)는 다음과 같이 계산한다.^[14]

\[\begin{aligned}\lambda&=\frac{y_2-y_1}{x_2-x_1} \\ x_3&=\lambda^2-x_1-x_2\quad(\text{mod }p) \\ y_3&=\lambda(x_1-x_3)-y_1\quad(\text{mod }p)\end{aligned}\]

이 덧셈 규칙은 기하학적 의미를 가진다. 점 \((x_1, y_1), (x_2, y_2)\)를 지나는 직선이 타원 곡선과 만드는 또 다른 점의 좌표가 \((x_3, y_3)\)이다. 또 덧셈 규칙과 더불어 무한원점 \(\mathcal{O}\) 라는 점도 정의하는데, 이는 일종의 0 역할을 한다고 생각하면 된다. 타원 곡선 위의 어떤 점이든 \(\mathcal{O}\)을 더하면 그 점 그대로의 결과가 나온다. 유한체로 제한한 타원 곡선 위의 점들과, \(\mathcal{O}\)를 이용하면 대수적 구조, 군^[15]을 정의할 수 있다. 군에 포함된 점들 중 아무거나 두 개 골라서 더하면 결과가 나오기 때문에, 한 점을 여러 번 더할 수도 있다. 여기서 타원 곡선 암호체계의 아이디어가 나온다. 타원 곡선의 파라메터(다항식의 계수, 유한체의 크기 등)을 정하고, 곡선 위의 어떤 점 \(G\)를 골라서^[16] 우선 표준으로 만든다. \(G\)를 어떤 횟수 \(n\)만큼 더하여 얻은 점 \(nG\)를 공개 키, 횟수 \(n\)을 비밀 키로 만든 다음, 비밀 키는 서명 생성에, 공개 키는 서명 검증에 사용하는 것이다. 이때 \(n\)과 \(G\)를 가지고 \(nG\)를 계산하는 것은 효율적이지만, \(nG\)와 \(G\)를 가지고 \(n\)을 계산하는 것은 이산 로그 문제로, 매우 어렵다. RSA가 RSA 문제의 어려움에 기초한다면, ECDSA는 이산 로그 문제의 어려움에 기초하는 것이다.

처음 우리가 한 생각은 "ECDSA 라이브러리는 많으니까 아무거나 하나 골라 써서 내도 되지 않을까?" 였다. 대회 문의를 했을때 외부 라이브러리를 사용할 수 있다고 했으니, 안될 이유는 없었다.

하지만 이렇게 간단하게 문제가 풀리지는 않았다.^[17] 디지털 서명에서는 서명할 데이터의 해시값을 입력받는다.^[18] 디지털 서명을 만들 때 SHA256과 같은 일반적인 해시 함수가 아닌, LSH 해시 함수를 사용하라고 명시되어 있었기 때문이다. 그래서 일반적인 ECDSA 라이브러리를 사용할 수는 없고, 직접 구현해야겠다는 결정을 했다.^[19]

ECDSA 라이브러리는 가장 편하게 사용할 수 있는 언어인 파이썬으로 구현했고^[20], 정상적으로 서명을 생성할 수 있는지 검증하기 위해 단위 테스트를 여러 개 코딩해서 검증도 직접 했다. 테스트를 코딩하면서 알게 된 사실이지만, 파이썬 cryptography 라이브러리의 cryptography.hazmat.primitives.asymmetric.ec를 사용하면 굳이 처음부터 구현하지 않아도 되었다. 그 시점에서는 ECDSA의 구현이 끝났고 (야속하게도) 테스트까지 모두 통과하는 상태였다. 역시 머리가 나쁘면 몸이 고생하는 법이다.

1, 2, 3번 문제를 해결하기 위해 작성한 코드는 Team Crypt0newbies 깃헙 저장소에서 확인할 수 있다. 혹시나 그럴 일은 없겠지만, 3번 문제를 해결하기 위해 작성한 ECDSA 코드는 일반적인 목적으로는 사용하지 않아야 한다. 이 ECDSA 구현은 side channel 공격을 당할 여지가 충분하고, 굳이 side channel 공격 때문이 아니더라도 비전문가이고, 암호학에 문외한인 사람이 작성했으며, 누구에게도 리뷰받지 않은 코드로 여러분의 디지털 서명을 생성할 필요는 전혀 없다.

이 대회를 참가하려는 후배들에게

자랑스럽게도, 이 포스트를 작성하는 날짜 기준으로 본다면 우리 학교는 2019, 2020, 2021년 대회 3연속으로 수상했다.

사실 일반적인 방법으로 이런 화면을 만드는 것은 불가능하다.

이제 여러분이 대회에 나갈 차례이다.

하지만 저는 암호에 대해서 아는 것이 없는걸요?

2020년 대회에 나갈 팀원을 구하려고 시도했을 때, 많이 들었던 거절의 이유^[21]는 "자신은 암호학을 모른다" 였다. 그런데, 정작 대회를 나가보니 암호학에 대한 사전 지식이 엄청나게 많이 필요하다는 느낌이 들지는 않았다. 당장 이 포스트 제목만 해도 "암호 뉴비들의 암호 깨는 대회 출전기"이다. 대회에 나가기 전에 암호학에 대해 정말 알아야 할 것은 암호가 무엇인지 정도뿐이었고, 나머지 지식은 대회를 참가하면서 알아가면 충분했다. 애초에 일반적인 고등학생 입장에서는 AES, ECDSA 등 암호학에 대한 세부적인 내용을 알 리가 없고, 대회 출제진도 이것을 고려하는 것으로 보인다.

또한, 이 대회가 5월 초부터 8월 말까지 3~4개월의 시간을 문제풀이에 할애할 수 있게 한다는 사실도 유념해야 한다. 암호분석경진대회에 출제되는 문제는 정보올림피아드나 수학올림피아드처럼, 몇 시간 정도에 풀라고 낸 것이 아니라 몇 달에 걸쳐 해결할 문제들이다.^[22] 또한, 문제를 풀기 위해서 전공 서적과 논문을 읽을 각오는 해야 한다.^[23] 이제 겨우 고등학생인데 적어도 대학교 수준은 되는 전공서와 논문을 어떻게 읽냐는 생각이 들 것이다. 처음 논문(과 전공서)을 읽을 때에는 정말 힘들다. 배경 지식도 전무하고, (적어도 내 경험으로는) 영어^[24]에도 익숙하지 않기 때문에 많이 헤멜 것이다. 하지만 이러한 어려움은 계속 논문을 붙잡고 있다 보면 어느 정도 자연스럽게 해결된다. 물론 대회 몇 번 나가는 정도론 전문가 수준을 기대할 수 없겠지만, 적어도 풀어야 하는 문제와 관련한 논문은 비교적 빠르게 읽을 수 있을 것이다.^[25]

대회에 참가해서 무엇을 할 지와는 별개로, 현실적으로 봤을 때 암호분석경진대회에 나가지 않을 이유는 충분하다. 여러분은 문제를 풀기 위해 몇 달 동안 3문제 정도를 가지고 고민할 것이고, 배워야 할 내용도 많을 것이다. (내가 느끼기에) 어려운 대회이고, 수상을 한다 해도 기록이 남거나, 대학교 입시^[26]에서 유리하게 작용하기는 힘들다. 이 대회를 하나의 스펙으로 생각한다면 문제를 해결하기 위한 노력에 비해 보상이 적을 것이다. 하지만 수학, 코딩을 좋아할 뿐만 아니라 이러한 단점을 감수하면서도 대회에 나가서 새로운 것을 배우며, 자신의 지식의 한계에 도전하고 싶다면 참가를 추천한다. 그런 이유로 참가했다면 대회 결과가 어떻든 좋은 경험이 될 것이다.

참고 문헌

• P. Morawiecki, "Practical attacks on the round‐reduced prince," IET Information Security, vol. 11, no. 3, pp. 146–151, 2017.
• 이인석, 대수학 (학부 대수학 강의 2). 서울, 관악구: 서울대학교출판부, 2008.
• D. Johnson, A. Menezes, and S. Vanstone, "The elliptic curve digital signature algorithm (ECDSA)," International Journal of Information Security, vol. 1, no. 1, pp. 36–63, 2001.

---

1. 사실 제대로 정신이 박힌 고3이라면 대회를 애초에 나가면 안 되는 거긴 하다. ↩︎

2. 난이도는 주관의 영역이기 때문에 실제로는 그렇지 않을 수도 있다. ↩︎

3. 첫 단어 첫 글자에서 초성, 둘째 단어 둘때 글자에서 중성... 이런식으로 쪼개서 만드는 규칙이 있을까에 대해서도 생각했지만 의미있는 답을 내지 못했다. ↩︎

4. Q&A 게시판에서 이어진 질문 끝에 주최측에서는 숨겨진 단어는 국가들과 연관되어 있다고 한다. 이러한 측면에서 볼 때 우리가 구한 답은 정답하고는 거리가 멀다. ↩︎

5. 아래 수식은 \(k_0\) 다음에 \(k_1\)을 덧붙여 \(k\)를 만들었다고 이해하면 된다. ↩︎

6. \(\ggg\)는 circular shift를 의미하는데, bit shift를 한 뒤 '잘려나간' 부분들을 앞의 빈 공간에 넣어준다고 생각하면 된다. ↩︎

7. 그림이 좌우 대칭인 것은 PRINCE 암호의 중요한 성질인 \(\alpha\)-reflection property를 암시한다. ↩︎

8. 미분과 적분의 관계를 떠올릴 수도 있겠지만, 더 흥미로운 것은 컴퓨터의 2진법 체계에서는 유한체 \(\mathbb{F}_2\)의 성질 때문에 모든 원소는 자기 자신의 덧셈 역원이고, 따라서 덧셈과 뺄셈이 똑같다는 것이다. ↩︎

9. 여기서 합은 배타적 논리합, XOR을 의미한다. ↩︎

10. 프로그래머용 계산기를 켜서, 16진수로 숫자를 입력해 본 다음 비트 전환 키패드로 숫자를 바꿔 보면 이해가 편할 것이다. ↩︎

11. 만약 \(2^{128}\)개의 키를 대회 기한 내에 계산할 수 있었다면, 암호분석경진대회 우수상이 아니라 튜링상을 받았을 것이다. ↩︎

12. 하나고등학교 와이파이를 사용한다면 비트코인 사이트가 차단되어서 볼 수 없을 것이다. ↩︎

13. 실제 사용되는 타원곡선은 이보다 훨씬 큰 유한체를 사용한다. 널리 사용되고 있는 파라메터인 secp256r1의 경우 유한체의 크기는 \(2^{224}(2^{32}-1)+2^{192}+2^{96}-1\)정도이다. ↩︎

14. 모든 계산은 \(\mathbb{F}_p\)에서 일어나기 때문에, 여기서 나온 나누기가 아니라 모듈로 역원을 구한 다음 곱하는 과정을 의미한다. ↩︎

15. 추상대수학에서 나오는 대수적 구조를 다 설명할 수는 없기 때문에, 이들에 대한 설명은 생략할 것이다. 여기서는 '덧셈이 가능한 집합" 정도로 이해하고 가면 된다. ↩︎

16. 당연한 이야기이지만 \(G\)로 \(\mathcal{O}\)를 고르면 안될 것이다. ↩︎

17. 뒤에서 설명하겠지만 문제가 간단하게 풀리지 않은 것은 나의 무지도 한몫 했다. ↩︎

18. 디지털 서명이 무엇인지 잘 모른다면 hashmm.com의 포스트를 보는 것도 좋을 것이다. ↩︎

19. 이미 있는 라이브러리의 코드 일부를 가져오고, 나머지는 우리가 구현하는 방식으로 할 수는 없는지 의문이 들 것이다. 하지만 오픈소스 코드의 라이선스에 따라 문제의 소지가 될 수 있고, 정정당당하게 문제를 풀이하는 대회에서 남의 코드를 그냥 사용하는 것은 좋은 방법이 아니라는 생각이 들었다. ↩︎

20. 처음에는 작성한 코드의 성능이 문제가 될 것을 걱정해 Rust나 Go, C++도 고려해 보았지만 가장 코딩하기 편한 언어를 고르다 파이썬을 사용하기로 했다. ↩︎

21. 물론 이것은 표면적인 이유이고, 실제 이유는 다를 가능성이 없지는 않다. ↩︎

22. 적어도 이 대회를 참가한 나의 입장에서는 그렇다는 것이다. 만약 이 문제들을 보고 "이거 3~4시간이면 풀겠는데?" 라는 생각이 드는 후배님이 계신다면 문제가 공지된 날에 다 풀어버린 다음, 새 역사를 쓰길 바란다. ↩︎

23. 이런 면에서 이 대회는 학교 시험과 같은 상황에서 요구되는, 순간적인 판단력보다는 자료들을 통해 문제 해결의 계획을 세우고, 자신이 사용할 수 있는 도구를 통해 답을 내는 과정을 차례차례 실행해 나가는 능력이 중요하다고 생각한다. ↩︎

24. 모르는 것이 생겨서 검색하면 알게 되겠지만 문제를 푸는 데 한국어로 된 자료를 찾는 것보다 차라리 여러분이 문제를 풀고, 한국어로 된 자료를 만드는 편이 더 쉬울 것이다. ↩︎

25. 슬픈 사실이지만 여러분은 문제와 관련된 지식을 아무런 배경 없이 익혔기 때문에, 이런 지식을 응용하는 데에는 제한적일 수밖에 없다. 그래서 논문 몇 편 읽었다고 암호학을 엄청 잘 안다는 착각에는 빠지지 말자. ↩︎

26. 이미 잘 알고 있겠지만, 상위권 대학교 입학이 인생의 최대 목표라면 이 대회를 나가지 않는 것을 추천한다. ↩︎