세상에 등장한 강력한 기하 암호, 타원곡선암호(Elliptic Curve Cryptosystem)
21세기 사회에는 컴퓨터와 무선 네트워크 기술이 발전함에 따라 원거리 통신, 다양하고 막대한 양의 정보 교환이 많아졌다. 잦은 통신으로 인해 중요한 개인 정보가 유출될 수 있는 기회 또한 많아졌으며, 이는 사실상 개인이 사회에 노출되었다고 해도 과언이 아니다. 해킹의 위협이 높아진만큼, 암호에 관련된 알고리즘 또한 많이 개발되고 있는 추세이다. 그 중 현재 기하적 원리를 바탕으로 설계된 타원곡선암호에 대해 소개하려고 한다.
타원곡선암호 알고리즘 원리
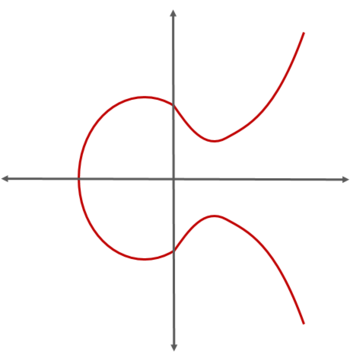
위에 있는 그림이 \(y^2 = x^3 - ax + b\)으로 표현할 수 있는 타원곡선이라 불리우는 곡선이다. 왼쪽 부분은 타원과 비슷한 꼴을 보이고 있으며, 오른쪽 부분은 각각 \(+\infty\)와 \(-\infty\)로 계속해서 발산하는 꼴을 보이고 있다. 타원곡선의 가장 큰 특징이라고 할 수 있는 것은 먼저 \(x\)축 대칭이라는 것, 그리고 임의의 직선에 대해 최대 3개의 교점을 가질 수 있다는 것이다.
가장 중요한 것은 타원곡선은 유한체라는 것이다. 유한체는 아래와 같이 정의된다.
집합에 속해 있는 원소의 수가 한정되어 있으며, 덧셈, 곱셈 연산에 대하여 닫혀 있는 집합
우리가 흔히 들어본 “닫혀 있다” 란, 연산의 결과 값도 집합에 속해있다는 것을 의미한다. 유한체를 사용하는 이유는, 암호연산은 정수를 기반으로 계산해야 하기 때문이다. 즉, 타원곡선이 암호학에 적합한 이유는, 실수(Real Number)상에서 연산을 하든, 유한체 상에서 연산을 하든, 동일한 수학법칙이 적용되기 때문이다.
이 특징들을 바탕으로 아래와 같이 타원곡선 암호의 알고리즘을 설계할 수 있다.
- 타원곡선 위에서 A라는 점을 잡는다.
- A를 지나는 임의의 직선을 긎는다.
- 임의의 직선과 타원곡선 사이에 생기는 교점을 \(x\)축 대칭시킨다.
- 대칭하여 생긴 점과 A를 지나는 직선을 다시 긎는다.
- 3번 과정과 4번 과정을 무한히 반복할 수 있다.
이렇게 A라는 점과 새로 생긴 교점 Z에 대해서 \(x\)축 대칭시키고, 새로운 직선을 긎는, 바로 이 과정을
A * Z
라고 정의하며, 이를 dot 연산이라고 한다.
이 알고리즘이 굉장히 혁신적이라고 말할 수 있는 까닭은 3번 과정과 4번 과정을 무한히 반복할 때 절대로 교점이 겹쳐지지 않는다는 점이다. 즉, 암호를 설계할 때 가장 중요한 일대일 대응 관계(암호화 - 복호화)를 만족한다. 그리고 dot 연산 자체에 제약 조건을 걸지 않는다면, 해당 알고리즘은 계속해서 dot 연산을 할 수 있을 것이다. 그렇기 때문에 이를 암호로 만들기 위해서는 하나의 제약 조건을 설정해줘야 하는데 그것이 바로 \(x_{max}\) 값을 도입하는 것이다. \(x_{max}\)는 새로 생긴 교점 Z의 \(x\)좌표를 의미한다. 즉, dot 연산을 반복하다가 새로 생긴 교점의 \(x\)좌표가 \(x_{max}\)와 일치한다면 이 때 알고리즘을 정지시키는 것이다. 그리고 이 때까지 dot 연산을 반복한 횟수를 \(n\)이라고 할 때, 바로 이 \(n\)이 암호를 생성하는 주요 키로써 작동한다.
실제로 해킹을 하는 사람 입장에서도 \(n\)을 찾기 힘들기 때문에 이 암호는 더욱 높은 보안력을 가진다. 다항함수가 아닌 이상 컴퓨터로 타원곡선과 직선 사이의 교점의 좌표를 구하는 것은 거의 불가능하다. 당장, 컴퓨터에 \(\cos(x) = 1/2\)의 해를 구하라고 시켜도 정확한 해를 찾지 못하고 수치적으로 근사한 해를 우리에게 제시한다. 수치적으로 해를 구하는 알고리즘은 다양하지만, 어떤 상황에서 어떤 알고리즘을 적용하느냐에 따라 시간복잡도가 달라지게 된다.
즉, \(x_{max}\)를 어떻게 정하느냐에 따라서 \(n\)이 달라질 것이고, 맨 처음에 어떤 기울기를 가진 직선을 그을 것인지에 따라서 dot 연산의 결과는 달라질 것이다. 다양하고 복잡한 과정이 녹아들어 있기 때문에 사용자로서는 보다 안전한 환경에서 통신 작업을 할 수 있고, 해커는 이를 뚫는 데 애를 먹을 것이다.
타원곡선 암호의 발전 가능성
타원곡선 암호는 위의 원리에서도 보았듯이 안전을 보장할 수 있는 암호체계이다. 하지만, 이 ECC 기술이 실생활에 아직은 적용하기 힘들 것 같다는 것이 여러 전문가의 견해이다. 타원곡선 암호가 워낙 고차원적인 지식을 요하기 때문에 전문적인 지식을 갖추고 있지 않은 개발자 등을 통해 구현될 수 없다는 것이다.
현재 타원곡선 암호는 비트코인 영역 등에서 실제로 적용되고 있다. 위에서 소개한 알고리즘을 바탕으로 Public-Key와 Private-key를 생성하여 실제로 통신을 할 수 있는 시스템을 구현한 것이다. 비트코인은 가상화폐, 즉 '돈'과 직접적인 관련이 있는만큼, 암호의 보안력 또한 높아야 한다. 즉, 타원곡선 암호는 보안력이 높은 암호임을 보여주는 셈이다.
이처럼, 타원곡선 암호의 발전 가능성은 무궁무진하다. 물론, 아직은 이 부분에 대해서 연구가 덜 되었고, 보다 전문적인 지식이 필요하긴 하지만, 훗날 타원곡선 암호를 바탕으로 돌아가는 세상이 오지 않을까 생각한다.
