벡터와 행렬의 활용 #2 고유값

고유값
행렬 A와 스칼라 λ에 대하여, A와 A의 고유벡터(eigenvector of A)를 곱한 행렬이 고유벡터의 스칼라 λ배와 같을 때, λ를 A의 고유값(eigenvalue of A)이라 한다.

특성방정식
A가 크기가 n×n인 대칭행렬일 때 A의 고유값은 실수가 나온다. 고유값이 존재할 필요충분조건은 det(A－λΙ)＝0인데, 이 때 이 다항식은 n차 다항식이 된다. 이 방정식을 행렬 A의 특성방정식이라 한다.

대각화 가능 행렬(diagonalizable matrix)

대각행렬과 닮은 행렬을 대각화 가능 행렬이라 칭한다. n×n인 정방행렬 A가 대각화 가능 행렬이기 위한 필요충분조건은 A가 n개의 '일차독립'인 고유벡터를 갖는 것이다.

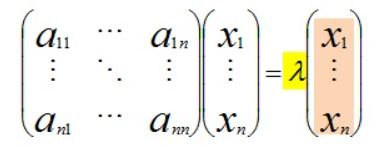
고유값 분해
고유값 분해는 한마디로 행렬을 고유값 및 고유벡터로 표현하는 것을 말한다. 대각화 가능 행렬만이 인수분해될 수 있다.

특이값 분해
선형대수학의 꽃이라 불리는 '특이값 분해'는 행렬을 직교행렬과 대각행렬로 분해하는 방법 중 하나이다. 일반적으로 정방행렬 여부와 관계 없이 모든 행렬에 대해 적용가능하다.

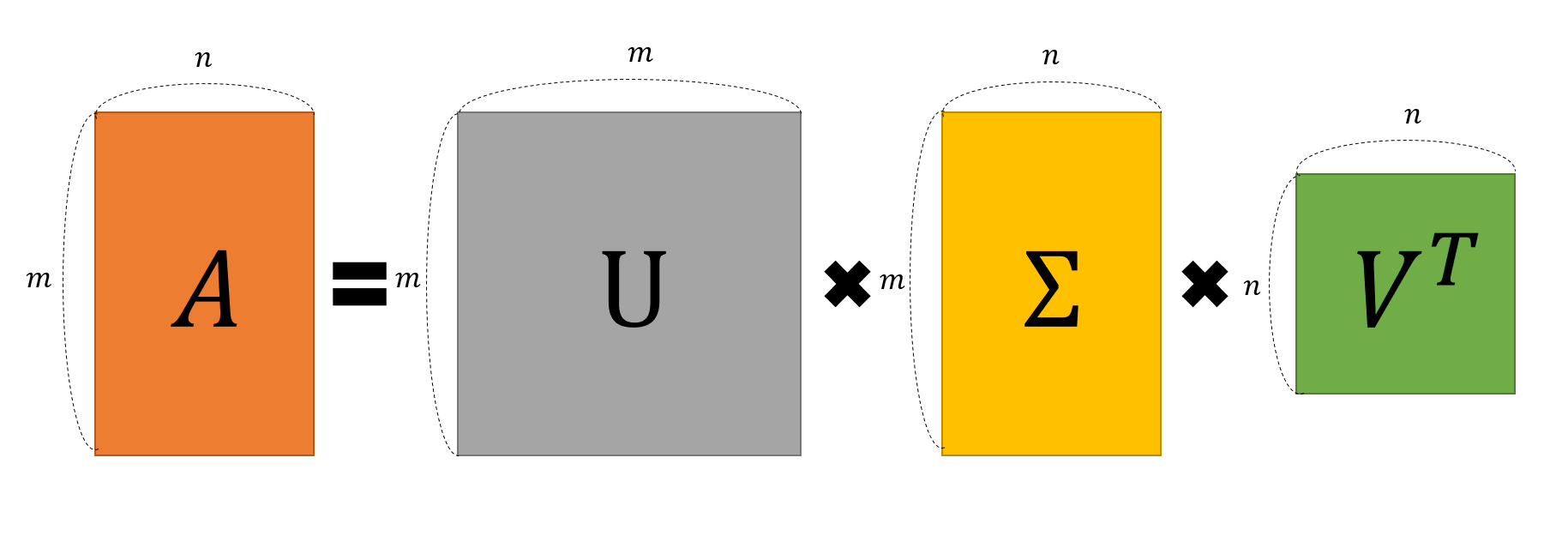
특이값 분해는 기상학, 컴퓨터 공학, 의학 등 여러 분야에서 활용되고 있다. 다음 시간에는 특이값 분해를 좀 더 자세히 다뤄보도록 하겠다.

참고문헌
[1] 기상학백과, https://terms.naver.com/entry.naver?docId=5863249&cid=64656&categoryId=64656
[2] 지형 공간정보체계 용어사전, https://terms.naver.com/entry.naver?docId=3475938&cid=58439&categoryId=58439
그림 1: https://angeloyeo.github.io/2019/08/01/SVD.html
표지사진: https://bskyvision.com/669