꼬인 위치에 있는 두 직선 사이의 거리는 어떻게 구할까?

이 글에서는 3차원을 넘는 \(n\)차원 세계의 벡터나 추상적인 기하학을 다루지 않는다. 직관적으로 이해하기 쉬운 3차원 상에서의 논의가 이루어질 것이다.

두 직선의 위치 관계

어떤 두 직선은 다음과 같은 4가지의 위치 관계를 가질 수 있다.

두 직선이 평행하다는 것의 정의는 두 직선의 '방향벡터'(단위벡터로 나타내었을 때)가 일치하며, 만나지 않는다는 것이다. 두 방향벡터가 일치함과 동시에 두 직선이 만난다면, 두 직선은 모든 점에서 만날 것이고 같은 직선이 된다.

직선의 방정식

일반적인 직선의 방정식은 \(ax+by+c=0\)의 형태를 가지는데, 이는 어디까지나 평면 상에서의 얘기이다. 3차원 이상의 공간으로 가게 되면, 모든 기하적 도형들을 벡터를 통해서 나타내는 것이 훨씬 수월하게 되는데, 3차원(그이상)의 공간 상에서 점 \(P\)을 지나고 방향벡터가 \(u\)인 직선의 방정식은 다음과 같다. \[\overrightarrow{OP}+t\vec{u}\] 이 식은 벡터의 합으로 이루어져 있는데, 원점\(O\)부터 점 \(P\)까지의 벡터에 방향벡터의 어떤 실수\(t\)배만큼 해준 벡터를 더하는 것이므로 점 \(P\)을 지나고 방향벡터가 \(u\)인 직선의 방정식이 된다.

정사영

이 개념을 소개하는 이유는 꼬인 위치의 두 직선 사이의 거리를 구하는데 매우 용이하게 쓰이기 때문이다. projection 의 의미를 가지고 있는데, 자세한 개념보다는 수식적인 차원으로만 접근하겠다. 벡터 \(\overrightarrow{A}\)에대한 벡터 \(\overrightarrow{B}\)의 정사영의 크기는 \(\frac{\overrightarrow{B}\cdot\overrightarrow{A}}{\mid \overrightarrow{A}\mid}\)이다.
이처럼 크기만 구하는 것은 '스칼라 사영'이라고 하고, '벡터 사영'이야말로 진정한  projection으로, 정사영한 방향벡터의 단위벡터를 곱해주면 된다. 벡터 \(\overrightarrow{A}\)에대한 벡터 \(\overrightarrow{B}\)의 벡터 사영은 \(proj_{A}B\)로 표기하며, \(proj_{A}B=\frac{\overrightarrow{B}\cdot\overrightarrow{A}}{\mid \overrightarrow{A}\mid}\hat{A}=\frac{\overrightarrow{B}\cdot\overrightarrow{A}}{{\mid \overrightarrow{A}\mid}^{2}}\vec{A}\)이다.

'거리'

우선 '거리'라는 것의 철학부터 이해할 필요가 있을 것 같다. 일반적으로 우리는 '유클리드 기하학'을 다룬다. 유클리드 공간에서 유클리드 거리는 '최단'의 의미를 가지며, '유클리드 거리함수'에 따른 거리를 말한다.
3차원 공간에 두 점 \(A\left(x_{1},y_{1},z_{1}\right),B\left(x_{2},y_{2},z_{2}\right)\)이 있다면, 유클리드 거리함수에 따른 두 점을 잇는 '벡터의 크기'라고도 생각할수 있으며, 다음과 같다. \[\mid\overrightarrow{AB}\mid=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}\]

고등학교 수학에서 배우는 점\(\left(x_{1},y_{1}\right)\)과 직선\(ax+by+c=0\) 사이의 거리는 다음과 같다: \[\frac{\mid ax_{1}+by_{1}+c\mid}{\sqrt{x_{1}^{2}+y_{1}^{2}}}\]  하지만 이는 평면 상에 있을 때의 얘기이다. 3차원 공간 상의 가면, 임의의 직선과 직선 밖의 한 점을 포함하는 평면은 단 하나 존재한다. 따라서 그 평면 상에서 계산할 수 있다. 3차원 공간 상에서 직선에 대한 수선의 발을 내리고, 그 수선의 발과 점을 잇는 선분의 길이를 마찬가지로 구하면 된다.

사실 \(\frac{\mid ax_{1}+by_{1}+c\mid}{\sqrt{x_{1}^{2}+y_{1}^{2}}}\)이라는 식의 의미는 매우 특별하고, 수학적이며 아름답다. 앞서 언급한 '직선의 방정식'과 '정사영'으로 이를 해석할 수 있으며, 평면과 점 사이의 거리로도 확장 가능하다.
일반적으로 직선의 방정식 \(ax+by+c\)는 \(\overrightarrow{OP}+t\vec{u}\)로 표현된다고 했다.
이때 점과 직선 사이의 거리 공식은 \(\mid\overrightarrow{OP}-\frac{\overrightarrow{OP}\cdot\vec{u}}{\mid\vec{u}\mid}\hat{u}\mid+\mid\vec{x}-\frac{\vec{x}\cdot\vec{u}}{\mid\vec{u}\mid}\hat{u}\mid\)라는 '정사영'을 이용한 공식과 다름이 없음을 알 수 있다.

3차원 상의 두 직선 사이의 거리

이러한 직선의 방정식을 바탕으로 3차원 상의 임의의 두 직선 사이의 거리를 구할 수 있다. 앞서 말했듯이, 공간 상에서 두 직선은 4가지의 위치 관계를 가진다.
i)일치하는 경우: 당연히 거리는 \(0\)이다.
ii)한 점에서 만나는 경우: 역시 당연히 \(0\)이다.

iii) 평행한 경우: 이때부터 조금 의미가 있다. 그러나 두 직선이 평행한 것은 한 평면 내에서 생각할수 있다.
앞서 언급한 직선의 방정식을 생각해보자. 두 직선이 평행한 것은 '방향벡터'가 같다는 뜻이다. 그러나 일치하지 않으려면 지나는 점이 달라야 한다. 따라서 두 직선 \(l_{1}\),\(l_{2}\)가 지나는 점을 각각 \(P_{1}\), \(P_{2}\)라고 하자.
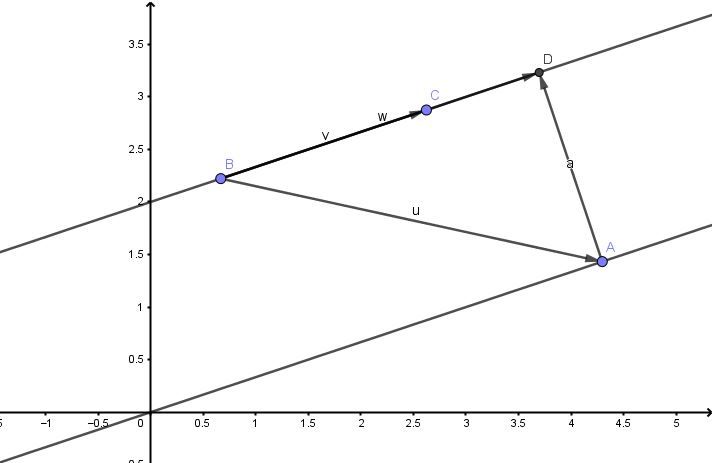
순차적으로 천천히 어떻게 구할지를 생각해 보자. 결국엔 한 직선의 임의의 점에서 다른 직선에 수선의 발을 내리면 된다. 이때 '수선의 발'이 키 포인트다. 이때 두 직선은 평행하므로, 방향벡터가 \(\vec{u}\)로 같다고 해보자. 그렇다면 직선 \(l_{2}\)위의 임의의 점 \(P_{2}\)에서 직선 \(l_{1}\)에 내린 수선의 발은 정사영을 이용해서, \(\overrightarrow{P_{1}P_{2}}\)라는 벡터에서 이벡터를 \(\vec{u}\) 벡터에 정사영한 벡터를 빼준 벡터의 '크기' 가 된다. 따라서 평행한 두 직선 \(\overrightarrow{OP_{1}}+t\vec{u}\)과 \(\overrightarrow{OP_{2}}+k\vec{u}\) 사이의 거리는 다음과 같다. \[\mid\overrightarrow{P_{1}P_{2}}-proj_{\vec{u}}\overrightarrow{P_{1}P_{2}}\mid\] 수식이 조금 복잡하므로, 평면 상의 그림으로 쉽게 이해할 수 있다. 아래 그림은 편이 상 평면 상의 두 직선으로 그린 것이지만, 벡터적으로 보았을 때 당연히 3차원에도 적용이 가능하다.

iv)꼬인 위치: 최종 목표는 임의의 두 직선 사이의 거리를 구하는 것, 즉 꼬인 위치에 있어도 거리를 구할 수 있어야 한다. 앞서 한 방법과 매우 유사하다. '정사영'을 이용하면 된다. 그런데 정사영을 해야하는 벡터를 어떻게 잡으면 좋을지 고민을 해야한다. 지금까지 생각한 벡터연산은 오직 '내적'(dot product)밖에 없었다. 그러나, 수선의 발을 내려서 정사영을 했다면 그 선분은 두 직선과 모두 수직인 선분이 된다. 그 선분의 길이만큼의 크기를 갖는 벡터라고 생각할수 있다. 그 벡터는 두 직선의 방향벡터와 동시에 수직이기 때문에 두 방향벡터가 생성하는 평면의 법선벡터, 즉 '외적'(cross product)으로 생성된 벡터가 될것이다.
따라서 그래도 적용하고, 두 방향벡터의 외적을 통해 얻은 평면의 법선벡터에 사영시키기만 하면 된다. 왜냐하면 평행한 직선에서는 두 방향벡터가 일치하기 때문에 외적하면 \(O\)이 되어 그 크기가 분모에 들어갈 수 없었다. 따라서 '벡터의 뺄셈'을 통해서 연산했지만, 외적벡터의 크기가 \(0\)이 아니면 분모로 들어갈 수 있으므로 그냥 사영해주면 된다.
따라서 평행하지 않은 두 직선 \(\overrightarrow{OP_{1}}+t\vec{u_{1}}\)과 \(\overrightarrow{OP_{2}}+k\vec{u_{2}}\) 사이의 거리는 다음과 같다. \[\mid proj_{\vec{u_{1}}\times\vec{u_{2}}}\overrightarrow{P_{1}P_{2}}\mid\]

'거리'에 대한 개념

고등학교 수학에서 배우는 거리, 길이 등에 대한 것은 결국 '벡터'의 크기이다. 모든 기하적 도형이나, 어떤 공간의 원소는 '벡터공간의 원소'인 '벡터'에 대한 해석으로 받아들일 수 있다. 직선 뿐만 아니라 평면 간의 거리, 곡선 간의 거리, 더 나아가 입체도형의 무게중심간의 거리, 곡면 사이에서의 거리 등 비유클리드 기하학까지 확장 가능하다. 이를 더 파헤치면 '사영기하학'으로도 접근할 수 있다. 기하학의 세계는 무궁무진하다.