[삼각형 시리즈 #1] 오일러가 사랑한 직선

수학 • 2021년 05월 31일

삼각형에 대하여

가장 적은 꼭짓점을 가졌으며, 가장 적은 선분으로 이루어진 평면 위의 도형은 무엇일까? 단순하기 그지없는 이 도형의 이름은 삼각형이다. 초등학교 때 등장한 이 도형은 중학생이 된 우리에게 피타고라스 정리와 삼각비, 외심·내심·무게중심, 심한 경우 수심과 방심이라는 머리 아픈 개념을 소개해주는 다리 역할을 한다. 삼각형과 관련된 내용이 없는 고등학교 교과서는 상상도 할 수 없을 정도다. 그렇다면 우리는 삼각형에 대해 얼마나 많이 알고 있을까? 피타고라스의 정리, 삼각비와 몇 가지 특징적인 점들만이 존재한다고 생각했다면 큰 오산이다.

오늘 소개할 오일러 직선에서 시작해 심슨의 정리, 제르곤의 정리, 체바의 정리 등 삼각형이 꽁꽁 숨기고 있던 특징들을 삼각형 시리즈라는 이름으로 낱낱이 드러낼 계획이다.

오일러 직선

삼각형의 오심을 아는 사람은 많을 것이라 생각한다. 수심, 방심의 특징까지 설명할 수 있는 사람은 많이 접하지 못했지만 대부분 다섯 점이 무엇인지는 알고 외심, 내심, 무게중심까지는 정확하게 설명하는 모습을 심심찮게 볼 수 있었다. 삼각형의 오심을 모두 아는 사람에게 질문을 던진다. 이 다섯 점들은 서로 연관돼 있을까? 다섯 점을 실제로 그려본 눈치 빠른 사람이 답하듯, 다섯 점들 중에서 연관돼 있는 점이 실제로 있다. 삼각형의 외심과 무게중심, 수심은 한 직선 위에 존재하는데, 우리는 이를 오일러 직선이라고 부른다.

세상에서 가장 아름다운 공식이라고도 불리는 오일러 공식의 그 오일러가 맞다. 그는 삼각형의 외심, 무게중심, 수심이 한 직선 위에 있다는 사실을 연구 끝에 밝혀내었고, 우리는 연구자 오일러의 이름을 붙여 오일러 직선으로 부르고 있다.

외심, 무게중심, 수심, 그리고 내심과 방심

오일러 직선에 대한 이해가 이루어지기 위해서는 앞서 설명한 오심의 정의에 대한 이해가 필수적으로 이루어져야 한다. 내심과 방심은 오일러 직선과 큰 관련이 없지만 삼각형의 특징적인 점이기 때문에 함께 소개하도록 하겠다.

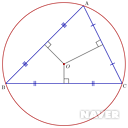
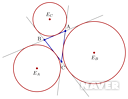
**그림 1~5. (왼쪽 위 사진부터 시계방향으로) 삼각형의 외심, 내심, 무게중심, 방심, 수심**

외심의 정의는 변의 수직이등분선의 교점이다. 외심으로부터 각 꼭짓점에 이르는 거리는 같다는 특징이 있다.

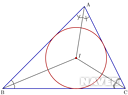
내심의 정의는 내각의 이등분선의 교점이다. 내심으로부터 각 변에 이르는 거리가 같다는 특징이 있다.

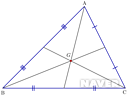
무게중심의 정의는 세 중선의 교점이다. 무게중심 작도 과정에서 만들어지는 6개의 삼각형은 면적이 동일하며 무게중심은 꼭짓점과 대변의 중점을 2:1로 내분한다.

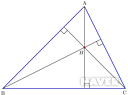
수심의 정의는 각 꼭짓점에서 대변에 내린 수선의 교점이다.

방심의 정의는 외각의 이등분선의 교점이다. 방심으로부터 삼각형의 한 변, 다른 두 변의 연장선까지의 거리가 같은 방접원을 생성한다. 한 삼각형에서 방심은 3개가 만들어진다. [1]

오일러 직선의 증명

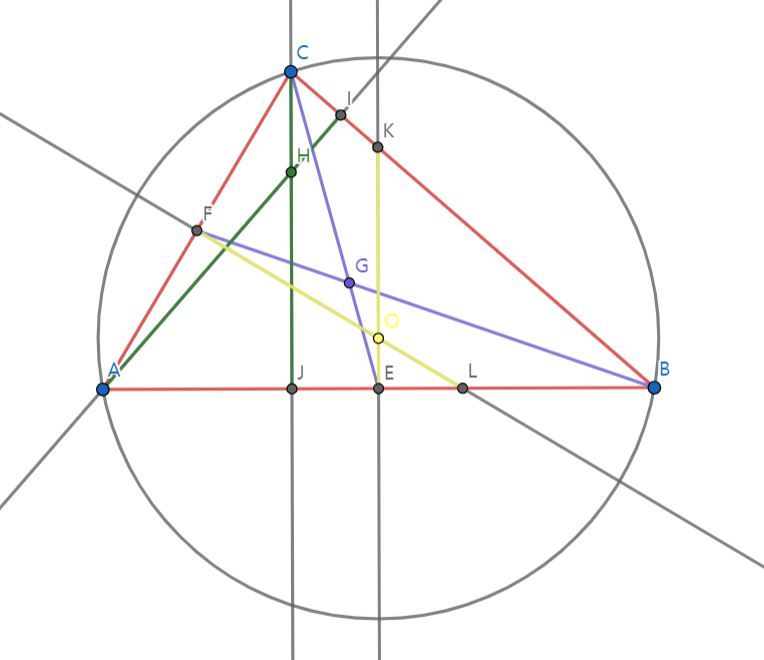
앞서 설명한 정의를 통해 삼각형 ABC 위에 수심, 무게중심, 외심을 나타냈다. Geogebra의 수직선과 수직 이등분선, 선분과 점을 그릴 수 있는 프로그램을 이용했으며 각 점을 구하는 데 사용되는 선분은 같은 색깔로 나타내었다. 삼각형에 외접하는 원은 외심을 중심으로 하는 점이며, 추후 증명에 사용된다.

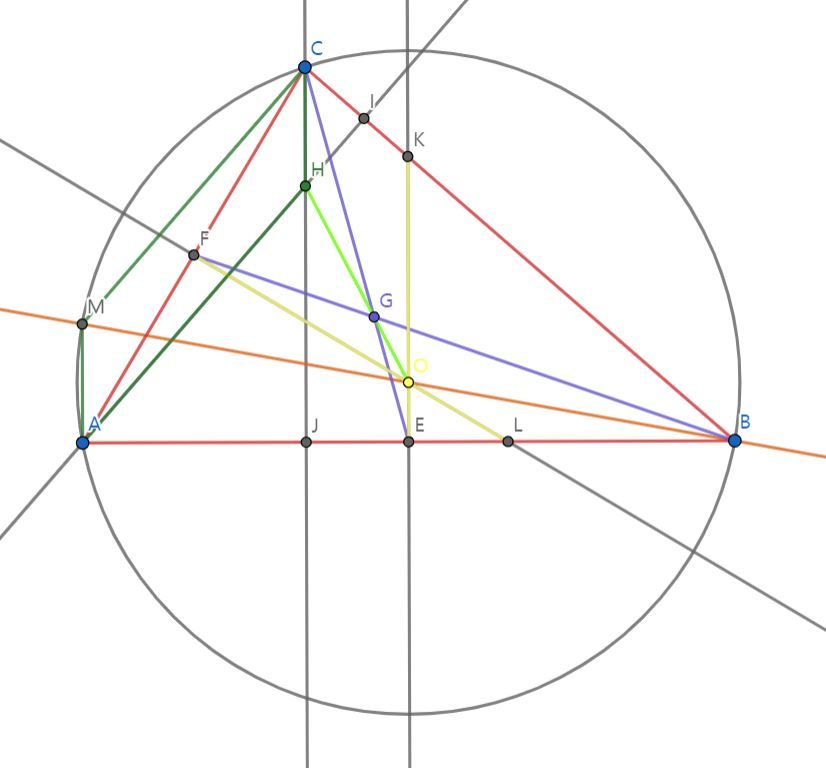
점 B에서 외접원 O의 중심 O을 지나는 직선을 그려 직선이 원 O와 만나는 B가 아닌 점을 M으로 두었다. 그 후 점 M과 점 A, 점 M과 점 C를 잇는 선분을 그렸다. 이 때 삼각형 MAB와 삼각형 MCB는 원의 지름을 한 변으로 하고 세 꼭짓점이 원 위에 있으므로 직각삼각형이며 ∠MAB=∠MCB=90° 이다. 여기서 선분 MA와 선분 CJ는 선분 AB에 대해 수직이므로 평행하고 선분 MC와 선분 AI는 선분 CB에 대해 수직이므로 평행함을 알 수 있다. 선분 MA⫽선분 CH, 선분 MC⫽선분 AH 이기 때문에 사각형 MAHC는 '두 쌍의 대변이 각각 평행한 사각형'의 정의를 가진 평행사변형이다. 평행사변형의 성질 중 '두 쌍의 대변의 길이가 같다'를 통해 선분 MA와 선분 CH의 길이가 같다는 것을 알 수 있다.

∠MAB=∠OEB=90°, 평행선의 성질에 의해 ∠AMB=∠EOB 이므로 삼각형 BOE∽삼각형 BMA (AA 닮음)이고 닮음비는 1:2이다. 따라서 선분 MA의 길이는 선분 OE의 길이의 2배이고 선분 MA의 길이와 선분 CH의 길이가 같으므로 선분 CH의 길이는 선분 OE의 길이의 2배이다.

무게중심은 꼭짓점과 대변의 중점을 2:1로 내분한다는 성질에 의해 선분 CG의 길이는 선분 EG의 길이의 2배이다. 또한 서로 평행한 선분 CH와 선분 OE, 선분 CE에 의해 생긴 엇각에 의해 ∠HCG=∠OEG 이다. 따라서 삼각형 HCG∽삼각형 OEG (SAS 닮음)이고 닮음비는 1:2 이다. 두 삼각형이 닮음이므로 나머지 두 각의 크기도 같음을 알 수 있고 선분 CH⫽선분 OE이며 ∠CHG=∠EOG 이기 때문에 선분 HO는 직선임을 알 수 있다. 이렇게 외심, 무게중심, 수심이 한 직선 위에 있다는 사실이 증명되었다. 여기에서 한 걸음 더 나가면 수심과 무게중심 사이의 거리가 무게중심과 외심 사이 거리의 2배임을 알 수 있다.

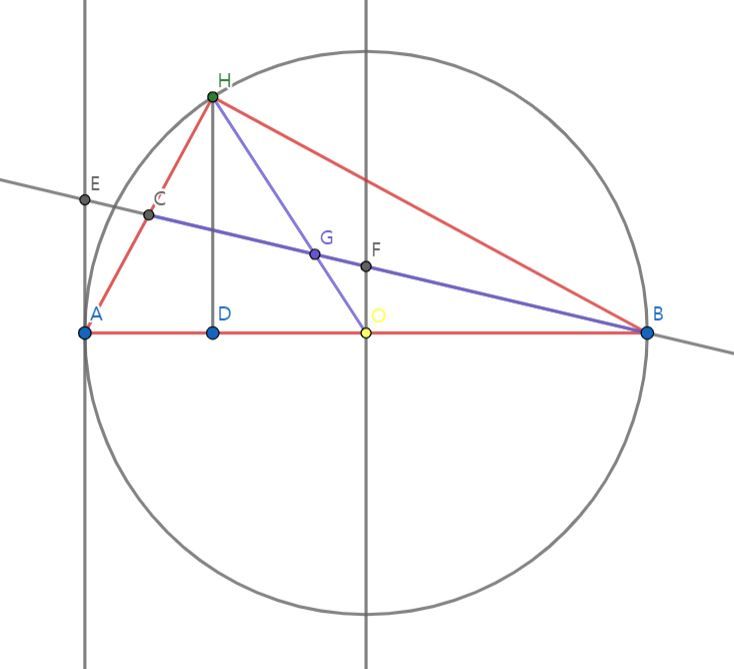
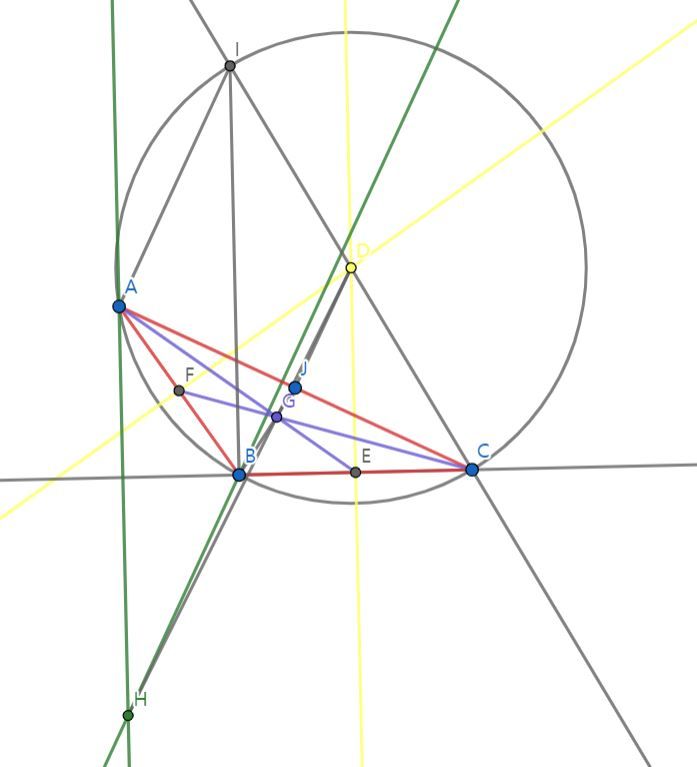
이전의 증명은 예각삼각형일 때 성립하는 증명이었다. 직각삼각형과 둔각삼각형에서의 증명은 위의 그림을 이용해 닮음 관계를 보이면 된다.

마치며

이번 기사를 통해 삼각형에서 외심, 무게중심, 수심 사이에 특별한 관계가 있다는 사실을 알게 되고, 다른 특이한 성질은 없나 궁금해하면 좋겠다. 오일러 직선을 증명하는 방법은 여러 가지이고, 제가 사용한 방법은 그 중 하나일 뿐이다. 더 학습하고 싶으신 분은 직각삼각형과 둔각삼각형에서의 오일러 직선을 증명해 보고, 다른 방법으로도 시도해보기 바란다.