[ 등하불명(燈下不明) 수학 #1 ] 유리함수와 쌍곡선의 관계
등하불명 수학에 대하여
등하불명(燈下不明) , '등잔 밑이 더 어둡다'라는 뜻을 가진 익히 들었던 속담입니다.
등하불명 수학은 여러분이 수학을 공부하는 과정에서 등잔 밑에 숨어 있어 미처 발견하지 못한 개념의 연결고리, 논리적인 증명, 적용되는 현상 등을 파헤치는 글이 될 것입니다. 등잔 밑의 '어두움'을 '밝음'으로 승화시킬 수 있는 좋은 기회가 될 것입니다.
그럼 본격적으로 첫 번째 주제인 유리함수와 쌍곡선의 관계에 대해 생각해봅시다.
유리함수
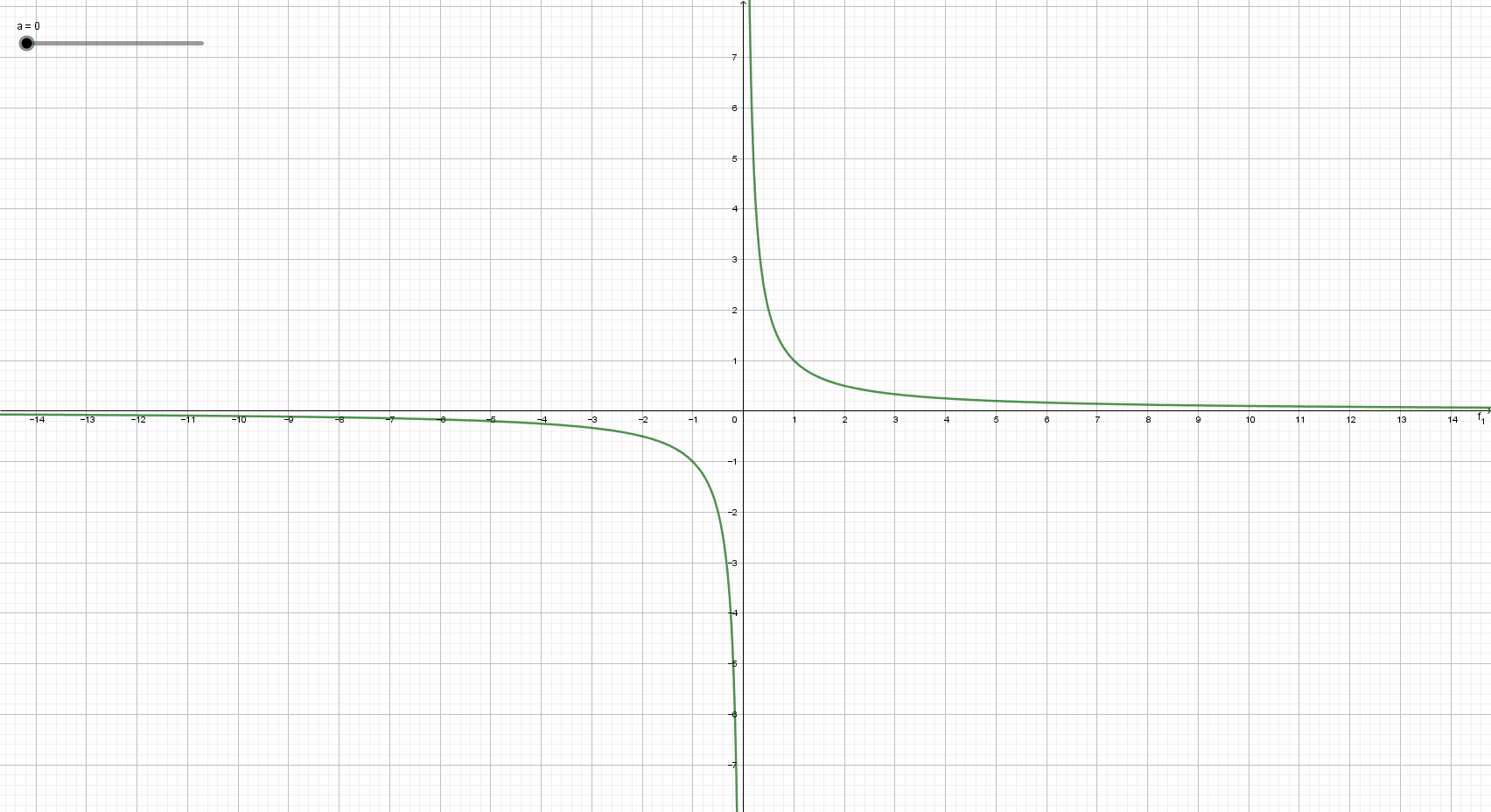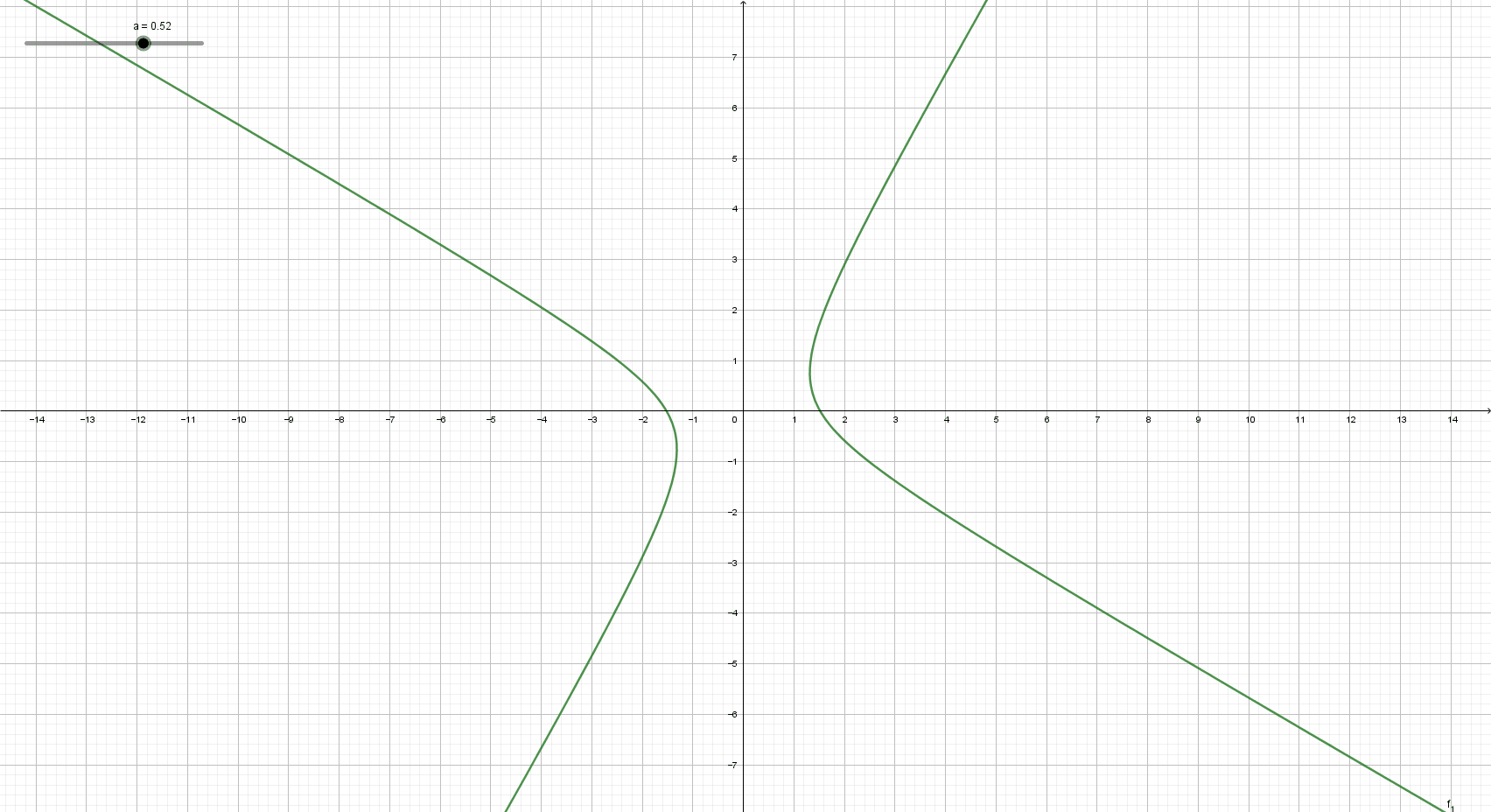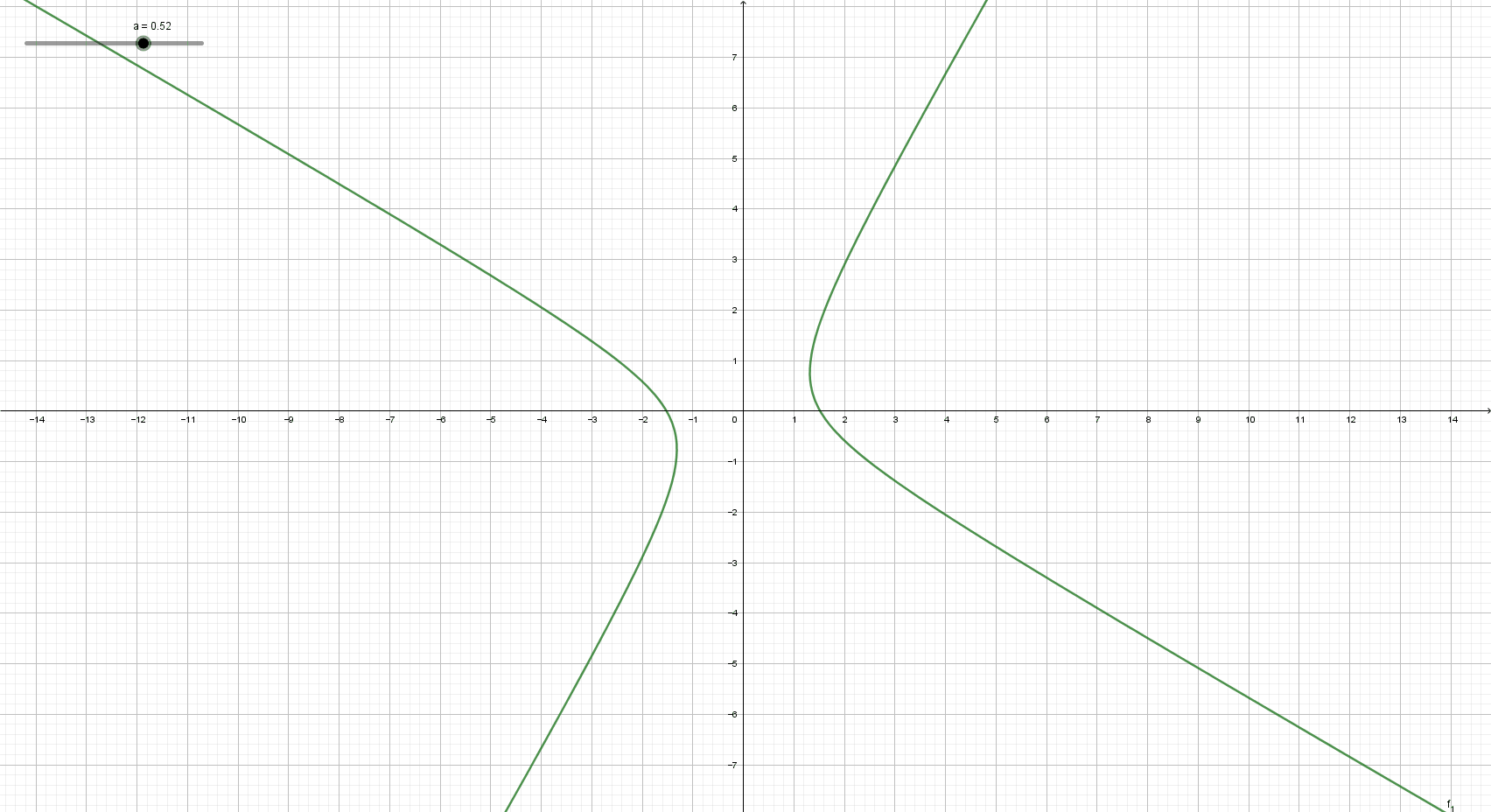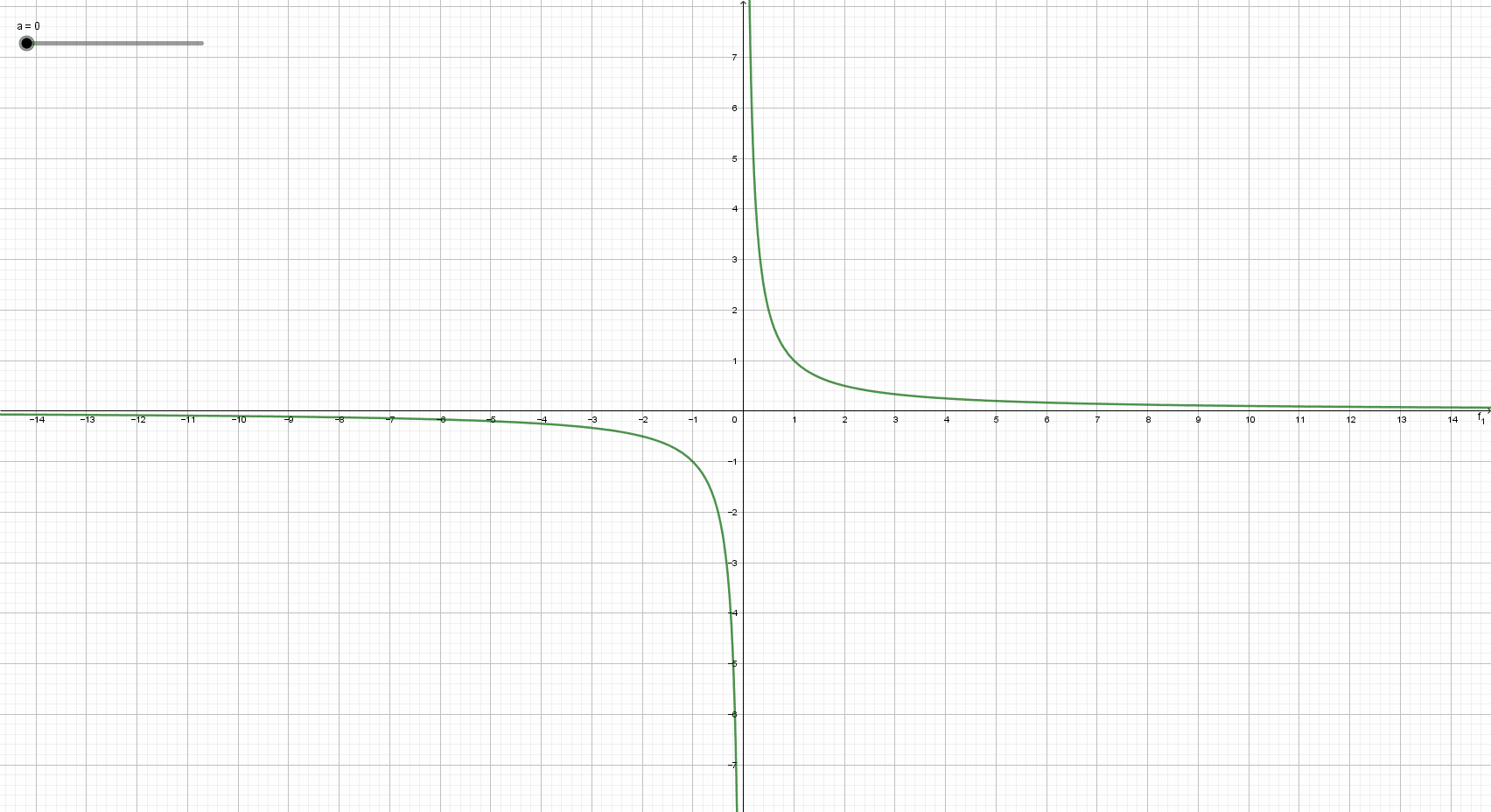
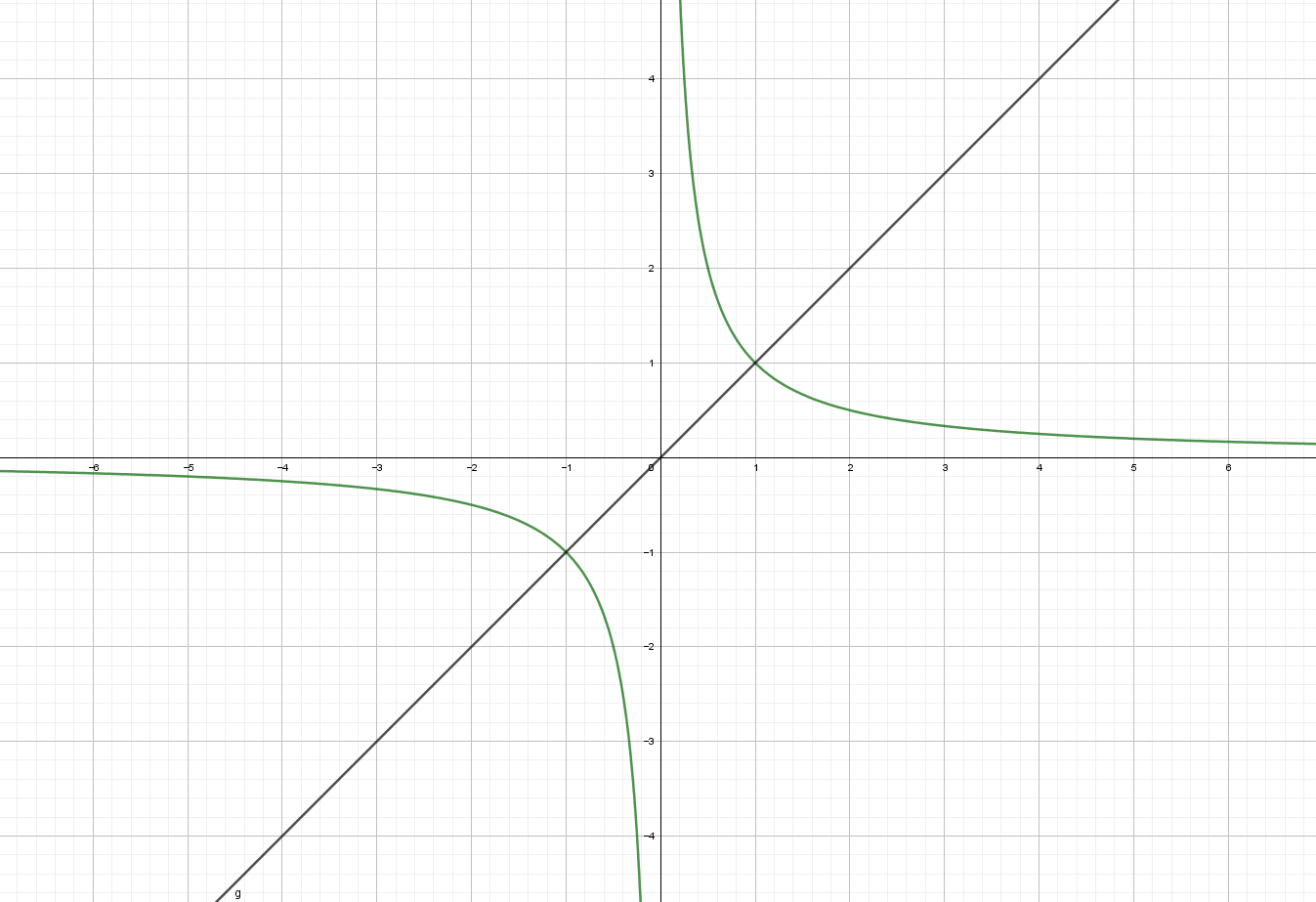
아마 대부분 유리함수를 고등학교 1학년 때 경험했을 것입니다. 유리함수는 그전까지 다루어왔던 다항함수와는 다른 성질들을 지니고 있습니다. 가장 대표적인 차이점은 바로 점근선의 유무이다. 이해를 돕기 위해 간단한 유리함수\(y =\) \(\dfrac 1 x\)를 그려봅시다.

위의 그래프를 보면
\(\lim\limits_{x \to \infty}f(x) = 0\), \(\lim\limits_{x \to- \infty}f(x) = 0\), \(\lim\limits_{x \to 0+}f(x) = \infty\), \(\lim\limits_{x \to 0-}f(x) =- \infty\)
임을 확인할 수 있는데, 이처럼 \(y =\) \(\dfrac 1 x\)은 \(x=0\)과 \(y=0\)이 점근선임을 알 수 있어요.
자 여기서 한 번 어둠에 갇혀 있는 기억을 상기해봅시다! 여러분이 아는 곡선 중에 위의 유리함수와 비슷하게 생겼으며, 두 개의 점근선을 가지고 있는 곡선이 있지 않은가요??
쌍곡선

쌍곡선은 위의 그림과 같이 두 개의 초점에서 임의의 점 P까지 선을 연결했을 때 두 선의 길이의 차가 일정한 성질을 가지고 있는 곡선입니다. 다시 말해,
평면상의 고정된 두 정점으로부터 거리의 차가 일정한 점들의 집합.
이라고 정의할 수 있습니다.
자, 그럼 이제 본격적으로 쌍곡선과 유리함수의 관계를 알아보겠습니다. 여기까지 읽으면서 어느 정도 알아채신 분도 있을 것이라 생각합니다. 직관적인 이해를 위해 유리함수를 회전시켜볼까요?
\(y =\) \(\dfrac 1 x\) 그래프를 회전시키다보면 위의 쌍곡선 그래프와 일치하는 모양이 나오게 됨을 확인할 수 있습니다. 즉, 유리함수는 곧 쌍곡선이며, 쌍곡선은 곧 유리함수라는 것을 알 수 있습니다. 직관적으로 이해가 되셨다면 보다 엄밀하게 쌍곡선이 유리함수임을 확인해보겠습니다.
유리함수가 쌍곡선임을 보이는 방법에는 두 가지가 있습니다. 위와 같이 유리함수를 화전시키는 행렬을 찾아 회전변환을 하여 확인하는 방법과 쌍곡선의 기본 성질인 두 정점에서 임의의 점까지의 거리의 차가 일정하다는 사실을 활요하는 방법이 있습니다. 이 글에서는 두 가지 방법을 모두 활용하여 증명을 해보도록 하겠습니다.
첫 번째 방법 - 회전 행렬 이용하기
우선, 계산을 간단화하기 위해서 쌍곡선 식을 \(\dfrac{x^2}{2}-\dfrac{y ^2}{2}=1\) 으로 특정하고, 증명을 해보도록 합시다. 이 증명 방법의 핵심은 다음과 같습니다. 쌍곡선 위에 있는 임의의 점을 설정합니다. 그리고 그 점을 원점을 기준으로 \(45\)\(^{\circ}\) 회전시켜 얻은 점의 자취를 유리함수 식과 비교해보는 것입니다. 굳이 \(45\)\(^{\circ}\) 회전시키는 이유는 우리가 알고 있는 유리함수 식의 꼴이 쌍곡선을 \(45\)\(^{\circ}\) 회전시켰을 때의 식과 일치하기 때문입니다. 자 그럼, 본격적으로 증명을 시작해볼까요?
먼저, 유리함수 위의 임의의 점을 \((x, y)\)라 합시다. 그리고, \(45\)\(^{\circ}\)회전시킨 점의 좌표를 \((x', y')\)이라고 합시다. 일반적으로 직교좌표계에서 원점을 기준으로 \(\theta\)만큼 회전시킨 행렬은 아래와 같이 나타낼 수 있습니다.
\(\begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix}\)
이 상황에서 \(\theta\) \(=\) \(45\)\(^{\circ}\)이므로, \((x', y')\)을 간단한 행렬곱으로 나타내보면 아래와 같이 나타낼 수 있습니다.
\(\begin{pmatrix} x' \\ y' \end{pmatrix}\)\(=\)\(\begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix}\)\(\begin{pmatrix} x \\ y \end{pmatrix}\)
행렬곱을 하여 계산을 하면
로 나오게 되고, 이를 다시 \(x\)와 \(y\)를 \(x'\)와 \(y'\)에 대한 식으로 바꾸어 주면
가 나오게 됩니다. (이 글에서는 연립을 활용하였지만, 위의 행렬식에서 역행렬을 곱해주는 방법으로도 구할 수 있습니다.) 이제, 각각 \(x\)와 \(y\)에 대한 식을 제곱하여 주면
이고, 이를 처음에 특정했던 쌍곡선 식에 대입해줍시다.
이를 정리해주면 결과적으로
가 나오게 되면서 쌍곡선과 유리함수가 같은 것임을 확인할 수 있습니다.
두 번째 방법 - 쌍곡선의 기본 성질 활용하기
이번에는 유리함수 \(y =\) \(\dfrac 1 x\)을 특정하고, 증명을 해보도록 합시다.
기본적으로 \(y =\) \(\dfrac 1 x\)은 \(y=x\)에 대해 대칭인 함수입니다. 즉, 만약 유리함수가 쌍곡선이라고 가정한다면 초점의 좌표 \(c = \sqrt{a^2+b^2}\)에서 \(a\)와 \(b\)가 동일할 것이기 때문에 \(c = \sqrt{2}a\)라 할 수 있어요.
이 상황에서는 \(a = \sqrt{2}\)이기 때문에 \(c=2\), 즉 초점의 좌표는 \(F(\sqrt{2}, \sqrt{2})\)와 \(F'(-\sqrt{2}, -\sqrt{2})\)라고 둘 수 있습니다. \(y =\) \(\dfrac 1 x\)위의 임의의 점 \(P(t, \dfrac{1}{t})\)을 두고 \(\overline{PF}\)와 \(\overline{PF'}\)을 구해봅시다.
이고, 결과적으로 보여야 할 것은 \(\overline{PF'}\)\(-\)\(\overline{PF}= constant\)이므로 \(t+\dfrac{1}{t} = s\)라 했을 때,
유리함수가 쌍곡선임을 가정하고 초점을 구해 임의의 점 P에 대해 거리의 차가 일정하게 나왔으므로 가정은 참임을 알 수 있습니다.
결론
오늘 알아본 내용을 간단하게 정리해봅시다. 우리는 교육과정 상에서 유리함수와 쌍곡선을 따로 배우게 되면서 자연스럽게 이 둘은 전혀 관계가 없다고 단정 지어왔습니다. 하지만, 실제로는 유리함수와 쌍곡선은 같은 곡선이며, 회전행렬에 의해 식의 꼴이 다를 뿐이라는 사실을 알게되었습니다.

이번 글을 통해 그리고 앞으로 등하불명 수학 시리즈를 통해 여러분 머리속의 '어두움'이 '밝음'으로 전환되기를 희망합니다.
