가짜 증가함수

서론

우리가 배우는 교과서는 각 학년 학생이 알아야 할 수학적 사실들을 정리함으로써 이해를 돕기 위해 제작된 것이어서, 수학적 엄밀성이 떨어지거나 수학적 사실과 동떨어진 경우가 종종 있다. 흔히들 말하는 대입에는 도움이 되지 못하더도 수학을 조금이라도 더 깊이 공부한 사람이라면 명확하게 알고 가는 것이 좋을 '증가와 감소'에 대한 이야기를 해보겠다.

2015 개정 교육 과정의 수학II를 공부한 사람이라면 증가 함수와 감소 함수가 무엇인지 안다. 하지만 이 때 배운 증가 함수와 감소 함수의 정의만 가지고는 가짜(?)로 증가하는 함수들 속에서 진짜로 증가하는 함수들을 판별해 내기 어렵다. 증가와 감소, 그리고 단조와 강한 단조 함수가 무엇인지 알아보며 머릿속에 명확한 수학적 정의를 탑재하자.

Monotonic Functions

함수가 단조롭다는 것이 무슨 뜻일까? '선생님의 목소리가 단조롭다'는 것은 곧 졸린 목소리라는 것이다. 어떤 특징이 일정하게 유지될 때 우리는 그것을 단조롭다고 여긴다. 단조 함수는 이와 마찬가지로 함수의 증감이 변하지 않는 함수이다. 다음은 함수 \(f: D \rightarrow C \)가 단조 증가 함수(monotonically increasing function)인 것의 수학적 정의이다 [1].

\(\forall x , y\) s.t. \(x, y \in D\)이고 \( x \le y\)이면, \(f(x) \le f(y)\)

이때 함수 \(f\)를 단조 증가(monotonically increasing)한다, 증가한다(increasing) 혹은 non-decreasing이라고 정의한다.

마찬가지로 단조 감소 함수(monotonically decreasing function)도 정의할 수 있고 이때의 함수 \(f\)를 단조 감소한다(monotonically decreasing), 감소한다(decreasing) 혹은 non-increasing이라고 한다.

\(\forall x , y\) s.t. \(x, y \in D\)이고 \( x \le y\)이면, \(f(x) \ge f(y)\)

이후 강한 단조 함수와의 비교를 위해 단조 증가 함수는 다음과 같이,

\(\forall x , y\) s.t. \(x, y \in D\)이고 \( x \l y\)이면, \(f(x) \le f(y)\)

단조 감소 함수는 다음과 같이

\(\forall x , y\) s.t. \(x, y \in D\)이고 \( x \g y\)이면, \(f(x) \ge f(y)\)

쓰는 것이 좋다. 물론 이 표현들이 이전의 정의와 동치인 이유는 '함수'이기 때문이다.

수학적 호기심이 있는 사람이라면 단조 증가\(\cdot\)감소 함수의 정의를 보고 다음과 같은 함수를 떠올릴 수도 있을 것이다.

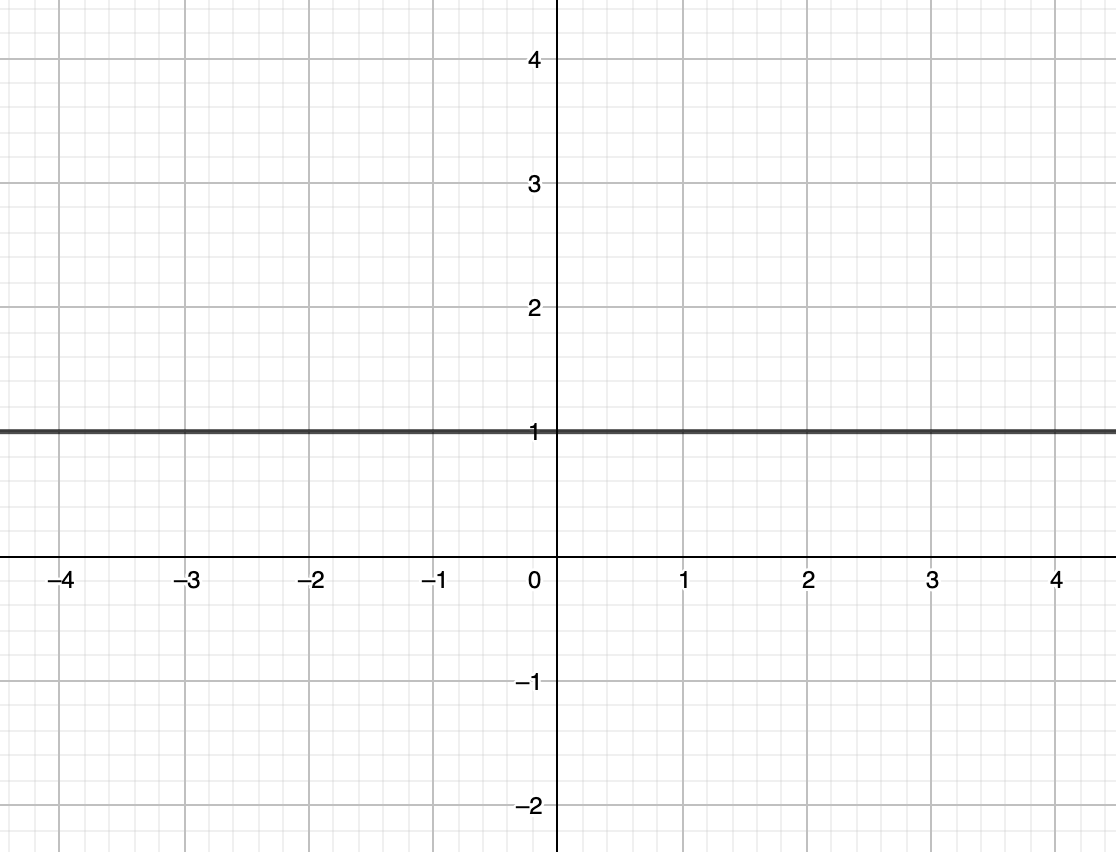
이 함수도 단조 '증가' 한다고 말할 수 있을까? 임의의 두 실수 \(x_1 \le x_2\)에 대해 \[f(x_1) = 1\le 1 = f(x_2)\] \[f(x_1) = 1\ge 1 = f(x_2)\]를 만족하기 때문에 단조 증가 함수이자 단조 감소 함수이다.

증가나 감소에 대한 우리의 직관과는 사뭇 다르다는 것을 느꼈을 것이다. \(f(x)=1\)를 보고 증가한다고 칭하지는 않듯이 말이다.

Strictly Monotonic Functions

단조 함수의 정의에서 불편함을 해소하고자 '등호'를 제거한 것이 강한 단조 함수(strictly monotonic functions)이다. 더 엄격한(strict) 조건을 지니고 있는 강한 단조 함수는 우리가 기대하는(?) 증가 함수와 잘 맞는다. 다음은 강한 단조 증가 함수(strictly monotonically increasing function)의 수학적 정의이다 [2].

\(\forall x , y\) s.t. \(x, y \in D\)이고 \( x \l y\)이면, \(f(x) \l f(y)\)

이와 유사하게 강한 단조 감소 함수(strictly monotonically decreasing function)도 정의할 수 있다.

\(\forall x , y\) s.t. \(x, y \in D\)이고 \( x \l y\)이면, \(f(x) \g f(y)\)

결국 단조 함수의 정의에서 \(x=y\)인 경우는 당연히 \(f(x)=f(y)\)이므로 \(f(x)=f(y)\)인 \(x<y\)를 허용하지 않는 것이 강한 단조 함수이다.

교과서와의 충돌

새로운 지식을 습득함에 있어 기존의 지식과 연결하는 것 만큼 중요한 것이 없다. 수학II시간에 배운 증가 함수와 감소 함수의 정의를 가져와 비교해보자.

볼 수 있듯이 현재 고등학교 교육과정에서는 증가와 감소를 단조 함수 대신 강한 단조 함수를 이용하여 정의하고 있다 [3], [4], [5].

미분 가능한 함수의 증가와 감소를 논하는 경우에는 구간의 모든 \(x\)에 대하여 \(f'(x)>0\)이 성립하는 함수 (혹은 구간의 모든 \(x\)에 대하여 \(f'(x)<0\)이 성립하는 함수, 즉 미분 가능한 강한 증가·감소 함수에 대해서만 언급하였다 [6].

위의 도표1. 를 수학적으로 말하자면 '증가·감소'는 '단조 증가·감소'로 보는 것이 맞다. 하지만, 고등학생의 입장에서는 강한 단조 함수로 증가·감소를 배웠기에 혼란이 발생할 수 있다. '단조 증가'나 '강한 단조 감소' 등의 표현은 말하고자 하는 함수를 정확하게 지칭하지만, 단순히 '증가'나 '감소'라고 했을 때 어떤 함수를 논하는 것인지 혼란이 생길 수 있다는 것이다.

특히, 수학II이나 미적분에서 나오는 함수 중 \(f(x)=x^3\)같은 함수들은 엄연히 단조 증가 함수이고, 심지어 강한 단조 증가 함수이지만, \(f'(0)=0\)이기 때문에 교과서에서 제시한 '미분가능한 함수의 증가·감소'로는 판별할 수가 없다.

결론

등호 하나의 문제로 지금까지 이야기해왔다. '친절한' 수학 표현은 단조, 강한 단조이겠지만, 증가나 감소라는 표현이 사용된다면 이는 단조 증가·감소 로 이해하는 것이 적절하겠다.

하지만!! 고등학생이라면 졸업할 때까지 강한 단조 함수만 증가·감소하는 것으로 받아들이자. 그리고 만약 문제에서 미분 가능한 증가 함수를 구하라고 하였다면, \(f'(x) \ge 0\)으로 식을 세워 풀고난 뒤 서로 다른 두 \(x_1, x_2\)에 대해 \(f(x_1)=f(x_2)\)인 것은 없는지 꼭 확인해 보자. 그런 두 \(x_1 \neq x_2\)가 있다면, 구하는 증가·감소 함수는 아닌 것이다.

참고문헌

[1] Monotone function. Encyclopedia of Mathematics. URL: https://encyclopediaofmath.org/index.php?title=Monotone_function&oldid=47894

[2] Monotonic function. Wikipedia. URL: https://en.wikipedia.org/wiki/Monotonic_function

[3] 황선욱, "도함수의 활용," in 고등학교 수학II, 미래엔, 2020, p. 81.

[4] 홍성복, "도함수의 활용," in 고등학교 수학II, 2017 검정, 지학사, 2020, p.83.

[5] 박교식, "도함수의 활용," in 고등학교 수학II, 동아출판, 2020, p.82.

[6] 홍성복, "도함수의 활용," in 고등학교 수학II, 2017 검정, 지학사, 2020, p.84.