[삼각형 시리즈 #2] 삼각형과 9개의 점

수학 • 2021년 06월 21일

[삼각형 시리즈 #1]에서 삼각형에서 나타나는 5개의 특징적인 점을 알아보았고 그 중 3개를 지나는 직선을 증명하였다. 이번에도 역시 삼각형에서 나타나는 특징적인 점 9개와 이 점들이 한 도형 위에 있다는 것을 증명하며 삼각형에서 발견되는 신기한 특징을 선보이겠다.

구점원

구점원은 삼각형에서 나타나는 9개의 점을 지나는 원이다. 9개의 점은 각각 각 변의 중점 3개, 각 꼭짓점의 수선의 발 3개, 각 꼭짓점과 수심을 잇는 선분의 중점 3개이다.

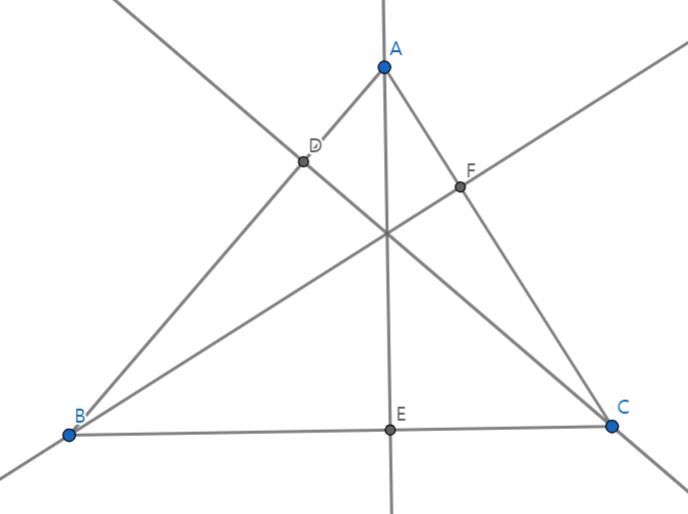
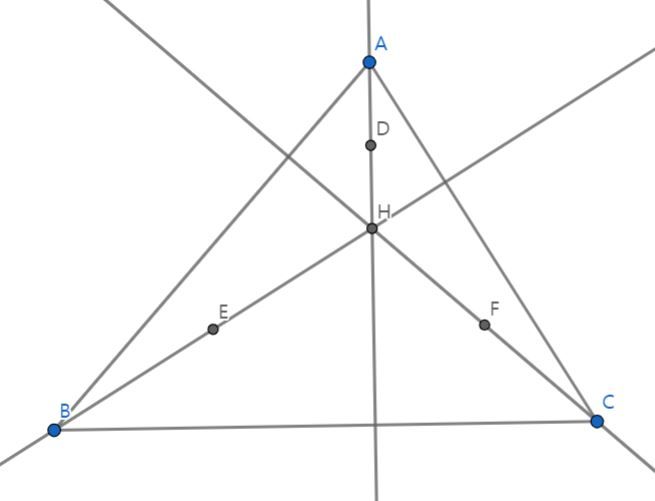
구점원의 증명

9개의 점이 한 원 위에 있다는 사실은 크게 세 과정으로 증명할 수 있다. 첫 번째 과정에서는 변의 중점 2개, 꼭짓점과 수심을 잇는 선분의 중점 2개, 꼭짓점에서 대변에 내린 수선의 발 2개가 한 원 위에 있음을 증명한다.

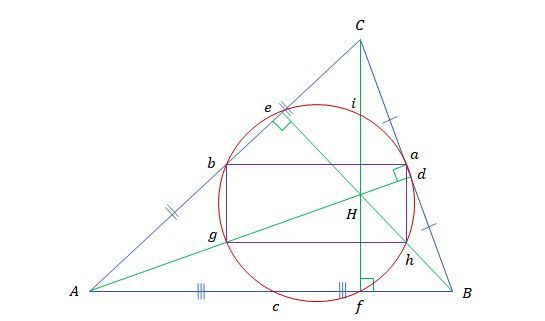
삼각형 AHC에서 b와 g가 선분 AC와 선분 AH의 중점이기 때문에 선분 bg는 선분 ch에 평행하고, 길이는 1/2이다. 같은 방법으로 삼각형 BHC에서 선분 ah는 선분 ch에 평행하고, 길이는 1/2이다. 따라서 선분 bg와 선분 ah는 평행하며 길이가 같다.

삼각형 AHB에서 선분 gh는 앞선 이유 때문에 선분 AB에 평행하고, 길이는 1/2이다. 또한 삼각형 ACB에서 선분 ba는 선분 AB에 평행하고, 길이는 1/2이다.

이때 선분 bg는 선분 Cf와 평행하고 선분 gh는 선분 AB와 평행한데, 선분 Cf와 선분 AB가 직교하기 때문에 선분 bg와 선분 gh가 이루는 각도는 90°이고 같은 방법을 통해 사각형 bgha은 내각이 모두 90°인 직사각형임을 알 수 있다. 따라서 선분 ga를 지름으로 하는 원에서 점 b와 점 h인 곳의 원주각이 90°이므로 점 b와 점 h는 원 위에 있다. 또한 ∠gda=90°이므로 점 d에서 원주각이 90°이고, 점 d가 원 위에 있다. 마지막으로 원에 내접하는 직사각형에서 두 대각선 모두 외접원의 지름이라는 사실을 통해 선분 bh가 지름이 되었을 때 ∠beh=90°이므로 점 e에서 원주각이 90°이고, 점 e가 원 위에 있다. 그림 4.를 통해 선분 ga, 선분 bh를 지름으로 하는 원 위에 점 b, g, h, a, g, e가 있음을 밝혔다.

두 번째 과정에서는 꼭짓점에서 대변에 내린 수선의 발 중 나머지 한 점이 앞선 원 위에 있음을 증명한다.

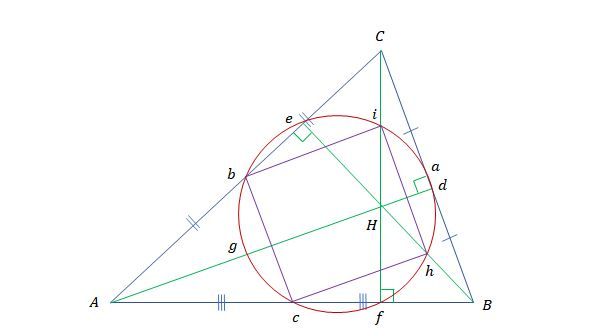
첫 번째 증명에서 직사각형임을 보인 것과 같은 과정을 통해 사각형 bchi가 직사각형임을 알 수 있다. 그림 5.에서 첫 번째 증명에서 원의 지름이라고 보인 선분 bh가 여전히 존재하기 때문에 첫 번째 증명에서 보인 것과 같은 크기의 원이 사각형 bchi에 외접함을 알 수 있고 선분 ci또한 지름이 된다. ∠cfi=90°이므로 호 ci에 대한 원주각은 90°로 점 f가 원 위에 있다.

마지막 과정에서는 앞서 보이지 못한 변의 중점 중 나머지, 꼭짓점과 수심을 잇는 선분의 중점 중 나머지가 원 위에 있음을 증명한다.

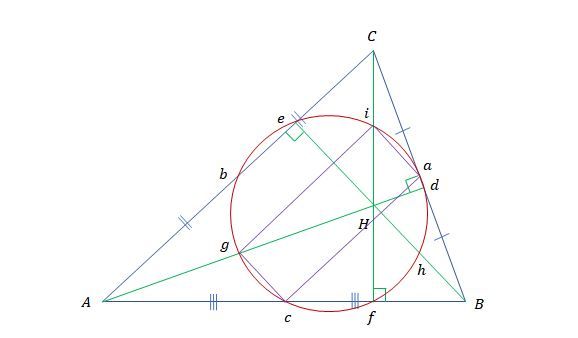
앞선 과정과 마찬가지로 사각형 gcai가 직사각형임을 보일 수 있다. 그림 6.에서 첫 번째 증명에서 원의 지름이라고 보인 선분 ga가 여전히 존재하기 때문에 첫 번째 증명에서 보인 것과 같은 크기의 원이 사각형 gcai에 외접함을 알 수 있고 선분 ci또한 지름이 돼 점 c와 점 i가 원 위에 있다. 마지막 증명의 경우 두 번째 증명에서 같이 해도 되겠지만 이 글에서는 첫 번째 증명으로부터 마지막 증명을 하고자 하였다. [1]

구점원의 증명은 시작일 뿐

삼각형에서 나타나는 9개의 점이 한 원 위에 있다는 사실의 증명은 시작에 불과하다. 사실 [삼각형 시리즈 #1]에서 소개한 오일러 직선에는 구점원의 중심도 포함되어 있다. 사실 구접원의 지름과 외접원의 반지름은 같다. 사실 구접원의 중심 위치를 증명할 수 있다. 사실 구접원은 내접원과 방접원에 접한다.

구접원 하나를 증명했을 뿐인데 여기서 파생된 새로운 사실들이 아주 많다. 삼각형의 신비함에 다시 한 번 놀라며 위의 새로운 사실들을 증명하러 떠나는 것은 어떨까.