[정수론101 #1] Legendre Symbol

들어가며

정수론에서의 관심사 중 하나는 이차 잉여이다.
[정수론1010 #0] Introduction에서도 말한 것과 같이 정수론에서는 나머지가 관심사이다. 어떤 정수를 다른 정수로 나눈 나머지를 관찰하다보면 두 수의 공약수도 구할 수 있고, 소수인지 판별할 수도 있다.

잉여계

'잉여'라는 단어는 '나머지'를 의미한다. 고로 '나머지'를 모은 것이 '잉여계'가 된다.
더 정확히 설명하자면, \(1\)보다 큰 자연수 \(n\)에 대해 \(0, 1, 2, \cdots, n-1 \)을 모은 집합은 n의 최소 양의 잉여계(least nonnegative residues modulo \(n\)) 이다.

하지만 \(n\)으로 나눈 나머지를 modulo \(n\)으로 나타냈을 때 꼭 음이 아닌 정수만 나올 필요가 없고, 5보다 작을 필요도 없다., 예를 들어 5의 최소 양의 잉여계는 \({0, 1, 2, 3, 4}\)이지만, \({-5, 1, 7, -2, -1}\)도 5로 나눈 나머지들을 modulo 5로 나타낸 것이기는 하다. 이와 같이 \(n\)으로 나눈 나머지들을 modulo \(n\)으로 나타낸 집합을 \(n\)의 완전 잉여계 (complete set of residues modulo n) 라고 한다.

n과 서로소인 나머지들은 어떨까? 3과 7는 서로소이기 때문에 7을 3으로 나눈 나머지인 1 또한 3과 서로소이다. 이와 같이 \(n\)의 완전잉여계의 원소 중 \(n\)과 서로소인 것들만 모은 집합을 \(n\)의 기약잉여계(reduced set of residues modulo n) 라고 한다.

이차잉여란?

이 잉여란 무엇인가? \(a\)가 \(n\)의 이차 잉여라는 것은 제곱을 \(n\)으로 나눈 나머지가 \(a\)가 되도록 하는 정수가 존재한다는 것이다.

즉, \(x^2 \equiv a \text{(mod n)}\)인 정수 \(x\)가 존재하면, **\(a\)가 \(n\)의 이차잉여 (제곱 잉여, quadratic residue)**라는 얘기이다.

이차 잉여라는 말이 존재한다는 것은 곧 이차 비잉여도 존재한다는 뜻이다. 모든 자연수가 어느 제곱수와 \(\text{mod n}\)에서 합동이 된다면, 굳이 이차 잉여라는 말이 존재하지 않았을 것이다.

예상한 것과 동일한 맥락에서 다음과 같이 이차 비잉여도 정의할 수 있다.

즉, \(x^2 \equiv a \text{(mod n)}\)인 정수 \(x\)가 존재하지 않으면, \(a\)는 \(n\)의 이차비잉여 (제곱 비잉여, quadratic nonresidue) 라고 한다.

앞서 이야기한 잉여계의 이론과 합치면, 자연스럽게 이차잉여계를 떠올릴 수 있다. 예상과 같이 \(n\)에 대해 \(x^2 \equiv a \text{(mod n)}\)인 정수 \(x\)가 존재하는 \(a\)의 집합을 \(n\)의 이차잉여계(quadratic residues modulo \(n\)) 라 한다.

몇가지 이차잉여

몇가지 이차잉여를 구해보면서 특징을 살피자.

가장 쉬운 modulo 2에서의 이차잉여를 구해보자.
mod 2에서는 모든 정수들이 홀짝으로만 분류되기 때문에 이차잉여가 0과 1 뿐이다.
\({0,1}\)이 mod 2의 완전 잉여계이면서 이차잉여계라고 할 수 있다.

하지만 modulo 3으로 가면 얘기가 달라진다.
mod 3에서는
\[0^2 \equiv 1 (\text{mod}3)\]
\[1^2 \equiv 1 (\text{mod}3)\]
\[2^2 \equiv 1 (\text{mod}3)\]
이므로 이차잉여계는 \({0, 1}\)이다.
즉, 2는 3의 이차비잉여이다.

유용하게 쓰이는 이차잉여는 modulo 4, 5, 8 등이 있다.
물론 여기서 유용하게 쓰인다는 것은 이차잉여계의 원소의 개수가 적은 것을 의미한다.

4의 이차잉여계는 \({0, 1}\)
5의 이차잉여계는 \({0, 1, 4}\)
8의 이차잉여계는 \({0, 1, 4}\)

\(m\)차 잉여

이차 이상의 다항식 \(x^m \equiv a \text{(mod n)}\)인 정수 a에 대해서도 논할 수 있다. 이런 경우에는
대표적 공식적인 용어는 아니지만 \(m\)차 잉여라고 부르자.

3차 잉여로는 7, 13이,
4차 잉여로는 13이 유용하게 쓰인다.

르장드르 기호

이차잉여와 이차비잉여는 단순하게 '나머지'라는 개념을 넘어서 아주 유용하게 쓰일 수 있다. 조금 더 간단하게 나타낼 수 있는 방법은 없을까?

이를 해결해 줄 수 있는 기호가 바로 르장드르 기호이다.
르장드르 기호는 다음과 같이 나타낸다.
\[\left ( {a \over n} \right )\].
여기서 정수 \(a\)가 소수 \(p\)와 서로소이고, \(p\)의 이차잉여이면, \(\left ( {a \over n} \right )=1\), \(p\)의 이차잉여가 아니면 \(\left( {a \over p}\right )=-1 \), \(a \equiv 0 (\text{mod} p)\)이면 \(\left( {a \over p}\right) = 0 (\text{mod} p) \)이다.

르장드르 기호는 오일러의 판정법(Euler's criterion) 에 의해 다음과 같이 정의할 수도 있다.
\[\left ( {a \over n} \right ) \equiv a^{p-1 \over 2} (\text{mod} p) \]이다.

몇가지 예

르장드르 기호를 이용하면 이창이여계에 속한 수들을 쉽게 표현할 수 있다.
지금까지 배운 것들을 조금 적용하면 다음과 같은 표를 만들 수도 있다.

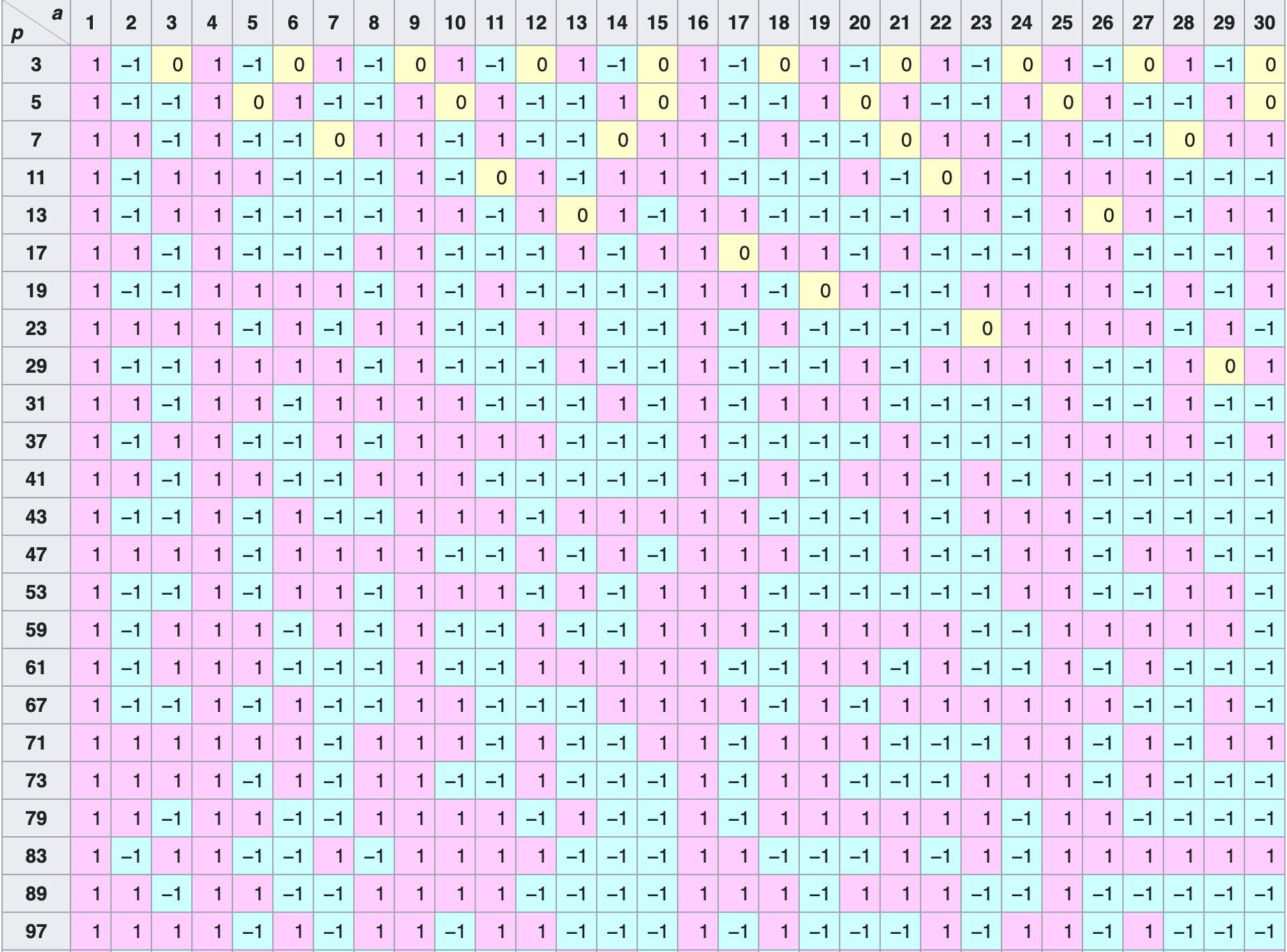
결국 르장드르 기호는 이차잉여와 이차 비잉여를 쉽게 나타내줄 수 있는 기호인데, 이 것은 다른 이론과 정리를 나타낼 때 유용하게 쓰인다. 이후에 [#2] 에서 르장드르 기호를 이용해서 \(p\)의 지수를 구할 수 있는 Lucas 정리에 대해서 알아보도록 하겠다.