\(\sin\left(\sin\left(\cdots\sin(x)\cdots\right)\right)=0\)

이 글은 \(\sin\left(\sin\left(\sin\left(\cdots\sin(x)\cdots\right)\right)\right)\)라는 함수, 즉 '\(0\)'이라는 상수함수에 대한 글이다. 삼각함수의 '무한 재귀함수'에 대해 알아보자.

'재귀함수'(Recursive function)는 컴퓨터 프로그래밍에서 자주 접할 수 있는 용어이다. 자기 자신을 반복하여 합성한 합성함수를 재귀함수라고 한다. 예를 들어서, \(f\left(x\right)=x^{2}\)이라는 함수가 있다면, 한 번 합성하면 \(f\circ f\left(x\right)=\left(x^{2}\right)^{2}=x^{4}\) , 한번 더 하면 \(f\circ f\circ f\left(x\right)=\left(\left(x^{2}\right)^{2}\right)^{2}=x^{8}\)과 같이 말이다.  수열의 점화식으로 이 재귀함수를 표현하는 매우 좋은 방법이 있는데, 바로 \(a_{n+1}=f\left(a_{n}\right)\)이다. 이 식은 입력값이 \(a_{n}\)항, 출력값이 수열의 그 다음 항인 \(a_{n+1}\)이고, 이값이 다시 입력값이 되어 \(f\)라는 함수에 계속 집어넣는다는 것을 수학적으로 명료하게 표현한다.

삼각함수를 무한 번 자기 자신에 대해서 합성하면 어떻게 될까? 앞에서 본 규칙을 똑같이 적용해 볼 수 있다. 대표적인 삼각함수 \(\sin x\)는 \(\sin\left(\sin\left(\sin\left(\cdots\sin(x)\cdots\right)\right)\right)\)가 된다. 그냥 수식적으로 봤을 때 전혀 감이 오지 않는다. 이 함수의 합성 횟수에 따른 그래프 변화 과정을 그림으로 나타내면 다음과 같다.

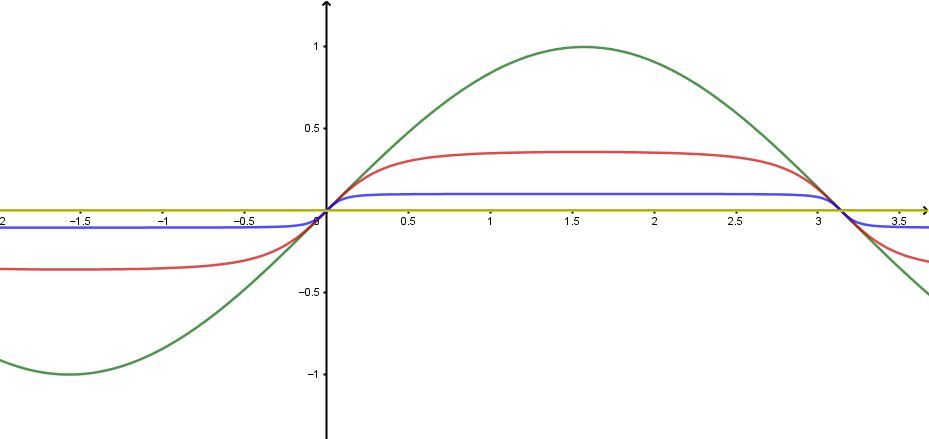
그림과 같이 \(\sin x\)함수가 진동하는 진폭이 작아지지만, 주기는 \(2\pi\)로 동일하며, 모든 지점이 마치 \(x\)축을 향해 다가가는 것 처럼 보인다. 그렇다면 직관적으로, \(\sin x\)의 무한 재귀함수는 \(0\)이라는 상수함수일 것이라고 합리적 의심을 해 볼 만하다.

'고정점'을 찾아라

수학에서 '고정점'이란 재귀함수에서 '입력값과 출력값이 같은 점'이다. \(a_{n+1}=f\left(a_{n}\right)\)일때, \(a_{n}=a_{n+1}\)이면 \(a_{n+1}=f\left(a_{n}\right)\)이므로 \(f\left(a_{n}\right)=a_{n}\)이다. 이때 \(\lim\limits_{n \rightarrow \infty}a_{n}=k\)라고 하면, \(f\left(k\right)=k\) 라는 방정식의 해, 즉 '재귀함수'와 '항등함수'의 '교점'이 '극한값'이 되는 것이다. 이 현상은 수학적으로 매우 아름다운 현상이다!

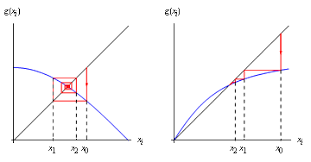
이를 \(\sin x\)에 적용해 보면, 다음과 같은 그림으로,  모든 \(a_{1}\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\)에 대하여 \(a_{n+1}=\sin\left(a_{n}\right)\)이면 \(\lim\limits_{n \rightarrow \infty}a_{n}=0\)이라는 것을 알 수 있다. 이는 극한값을 \(k\)라고 놓았을 때, \(\sin k=k\)인 \(k\)가 \(0\)밖에 존재하지 않기 때문이라고도 할 수 있다.

과연 모든 점에서 \(0\)인가

앞서 언급한 고정점 반복법으로 무한재귀함수를 구하는 것은 \(a_{1}\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) 일때이고, 이는 직관적으로 쉽게 와닿는다. 왜냐하면 \(y=x\)와도 가깝고 교점이 직접적으로 보이면서, \(0\)으로 다가가는 것이 보이기 때문이다. 그러나 임의의 실수 \(a_{1}\)에 대해서도 \(\sin\) 무한재귀함수가 \(0\)일까?  이 논의는 너무 간단하다. \(a_{1}\)이 어떤 값일지는 처음에 모른다. 그러나 \(f\left(x\right)=\sin x\)라는 함수는 '정의역(domain)'은 실수 전체 집합이지만, '치역(range)'이 \(-1\)부터 \(1\)까지의 실수만을 가진다. 즉 \(a_{1}\)이 어떤 값이든 간에, \(a_{2}\)부터는 반드시 \(-1\)과 \(1\) 사이의 값이라는 것이다. 이때 \(1<\frac{\pi}{2}\) 이므로 처음 고정점을 논했을 때의 범위인 \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\)는 \(\sin x\) 함수의 치역인 \(\left[-1,1\right]\)을 포함하는 범위이므로, \(a_{1}\)의 값에 관계없이 \(a_{2}\)부터 고정점에 대한 논의를 해도 함수열의 수렴성에 대한 논의에는 전혀 지장이 없다. 아니면 \(a_{1}\)을 \(a_{0}\)라는 상수로 놓고 한번\(f\left(x\right)\)에 입력하여 얻은 값을 \(a_{1}\)이라고 생각하고 그때부터 시작하는 것과 같은 원리일 것이다. 따라서 \(a_{1}\)에 관계없이 \(a_{n+1}=\sin\left(a_{n}\right)\)이면 \(\lim\limits_{n \rightarrow \infty}a_{n}=0\)이다.

\(\cos\left(\cos\left(\cos\left(\cdots\cos(x)\cdots\right)\right)\right)\)

\(y=\sin x\)와 \(y=x\)가 만나는 교점은 \((0,0)\) 이다. 하지만 \(\cos x=x\)의 해는 수치적으로만 구할 수 있고, 일반적인 해는 정확한 값을 구하는 것이 불가능하다. 이 값을 \(alpha\)라 하자. 그렇다면 \(\cos\left(\cos\left(\cos\left(\cdots\cos(x)\cdots\right)\right)\right)\)역시 상수함수로 수렴할텐데, 이는  \(\cos x=x\)의 유일한 해인 \(alpha\)라는 상수함수로 수렴할 것이다.이 알파 값은 대략 \(0.74\) 정도이다.  \(\cos x\)에 대한 무한 재귀함수는 \(a_{n+1}=f\left(a_{n}\right)\) 이라는 식에서 \(f\left(x\right)\)를 \(\cos x\)로 바꾸어줘도 상관 없지만, 이미 \(f\left(x\right)\)를 사인이라고 정해놓은 상태이기 때문에 또다른 수학적 기술로  \(\sin\left(\frac{\pi}{2}-x\right)=\cos x\)라는 점을 이용하여 \(a_{n+1}=f\left(\frac{\pi}{2}-a_{n}\right)\)으로 나타낼 수 있다. 이렇게 되면 입력값을 계속 넣어줌에 따라서 재귀함수를 실행할 때 마다 \(f\left(x\right)\)인 \(\sin x\)가 \(\cos x\) 로 바뀌어서 출력값을 도출하게 된다. 따라서 우리는 \(a_{n+1}=\cos\left(a_{n}\right)\)이면 \(a_{1}\)에 관계없이 \(\lim\limits_{n \rightarrow \infty}a_{n}=\alpha\)임을 알 수 있다. 아래 사진은 \(\cos x\)의 무한 재귀함수 수렴 과정이다.

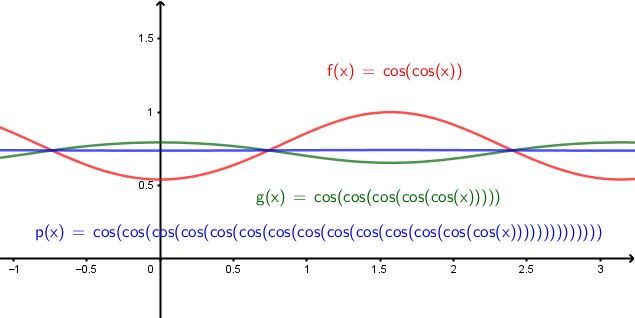
다양한 함수들의 무한 재귀함수

이 글에서는 사인과 코사인에 대해서만 무한재귀함수의 그래프를 보았다. 이 함수들은 '상수함수'로 '균등수렴'한다는 점에서 매우 특징적이며, 직관적으로 떠올리기 어렵지 않다. 하지만 또다른 합성 규칙을 가지고 재귀함수를 생성할 때, 그 함수열의 수렴성과 균등수렴 여부는 또다른 얘기가 된다. '균등수렴'이 무엇인지에 대하여 아래 링크를 참조하길 바란다.

https://ko.wikipedia.org/wiki/%EA%B7%A0%EB%93%B1%EC%88%98%EB%A0%B4