벡터와 행렬의 활용 #1 벡터, 행렬과 고유값
벡터와 행렬
벡터와 행렬의 활용 시리즈에서는 벡터와 행렬이 무엇이고 다양한 분야에서 어떻게 활용되는지와 관련된 심화개념을 다룰 예정이다. 이번 시간에는 벡터와 행렬이 무엇인지부터 알아보겠다.
벡터
벡터에 대해 먼저 알아보자.
벡터는, 특히 선형대수학에서, 단순히 크기와 방향을 가진 물리량을 나타내는 것은 아니다.
벡터가 무엇이냐 물으면 '벡터공간의 원소'라고 하는 것이 정확한 표현인데, 그렇다면 벡터공간은 무엇일까?
벡터공간
집합 V와 실수 전체 집합 R에 대해, 임의의 V의 원소 u와 v, 임의의 R의 원소 a를 생각하자.
첫 번째로, 'u와 v를 더한 것이 V의 원소이다'를 만족하고
두 번째로, 'au가 V의 원소이다'를 만족할 때 우리는 V를 '벡터공간'이라 부른다.
이렇게 정의된 벡터공간의 원소 u,v,w와 R의 원소 a,b는 다음과 같은 성질을 만족한다.
- 덧셈에 대한 교환법칙 u+v=v+u
- 덧셈에 대한 결합법칙 (u+v)+w=u+(v+w)
- 덧셈에 대한 항등원 존재 ∃0∈V, 0+u=u
- 덧셈에 대한 역원 존재 ∃u∈V, u+(-u)=0
- 스칼라곱에 대한 결합법칙 a(bu)=(ab)u
- 스칼라곱에 대한 분배법칙 (a+b)u=au+bu
- 스칼라곱에 대한 항등원 존재 ∃1, 1u=u
행렬
그렇다면 행렬은 무엇일까?
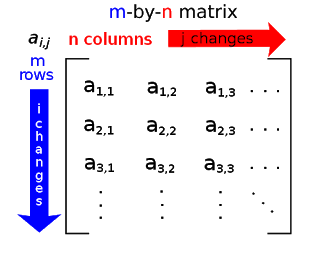
위와 같이 수를 배열한 것을 행렬이라 한다.
위 그림과 같을 때 m을 행의 수, n을 열의 수라 할 수 있다.
i번째 행과 j번째 열의 공통부분을 (i,j)항이라 한다.
행렬과 벡터
행렬의 합과 상수배는 행렬을 원소로 하는 집합에 대해 닫혀있는데, 단순히 합과 상수배 이외에도 행렬곱 또한 벡터와 연관성을 가진다. 행렬 A와 B의 곱 AB를 나타내는 행렬의 i번째 행과 k번째 열에 있는 항은 A의 i번째 행벡터와 B의 k번째 열 벡터를 내적한 값이라 할 수 있다.
고유값
마지막으로, 좀 더 심화적인 개념으로 고유값에 대해 소개하겠다.
행렬 A와 영벡터가 아닌 벡터 x에 대해, 스칼라 a에 대해 Ax=ax가 되는 a를 A의 고유값(eigenvalue of A)이라 한다. 이 때 x를 a에 대응하는 A의 고유 벡터(eigenvector of A)라 한다.
관련된 개념으로는 대표적으로 특이값 분해(SVD, Singular Value Decomposition)이나 주성분분석(PCA, Principal component analysis)가 있다. 다음 기사에서는 벡터와 행렬의 활용 방법에 대해 본격적으로 알아보겠다.
참고문헌
[1]https://terms.naver.com/entry.naver?docId=3475938&cid=58439&categoryId=58439
[2]https://terms.naver.com/entry.naver?docId=1101584&cid=40942&categoryId=32225
