연속근사법과 고정점 정리

산-염기 문제

고급화학 수강생이라면, 산-염기 문제를 푸는 도중 이차방정식을 자주 맞이했을 것이다.
Oxtoby 교재 문제 중 연속근사법이 쓰인 문제를 가져와 봤다.

이 문제는 그냥 이차방정식을 풀면 된다. 그러나 수학하는 사람들은 계산이 복잡한것을 매우 싫어한다. 물론 공학용 계산기가 있지만, 우리는 이차방정식을 근의 공식으로 직접 푸는것 만큼은 피하기 위해서 '연속근사법'이라는 것을 배웠다.

연속근사법

연속근사법이란, 위 문제를 예시로 들자면, 처음에는 분모를 무시한 채
\(\frac{y^{2}}{0.00100}=1.76\times 10 ^{-5}\)으로 계산하여 \(y\)값을 얻는다. 이때, \(y=1.33\times 10 ^{-4}\)이다. 다시 분모에 이 값을 넣고,
\(\frac{y^{2}}{0.00100-0.000133}=1.76\times 10 ^{-5}\)를 계산한다. 이것을 반복하여 원하는 유효숫자의 범위 안에 들어올 때 까지 계산하면, 근삿값을 얻을 수 있게 된다.

그런데 도대체 이 원리가 무엇일까?

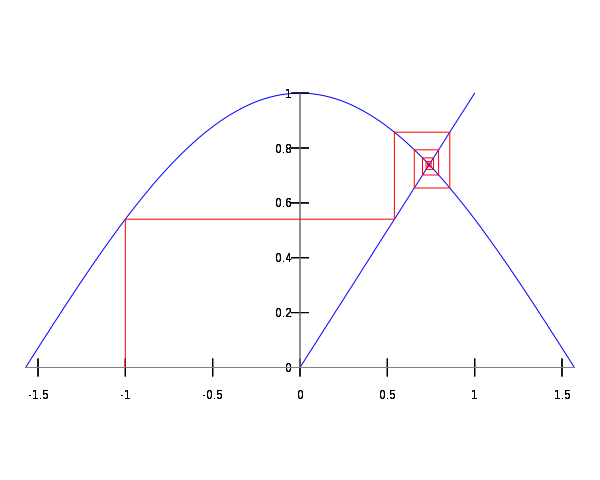
고정점 도형

바로 [고급수학]시간에 배운(?) '고정점 도형'에 있다. 고정점으로 수렴하는 수열을 잡는 것이 바로 연속근사법의 원리이다.  우리가 여태 한 것을 수학적으로 나타낼 수 있다. 바로 수열을 통해서다. 수열 \(a_{n}\)을 다음과 같이 정의한다. \[a_{n+1}=f\left(a_{n}\right)\] 이때 \(f(x)\)는 연속근사법을 위한 함수, 무리함수가 된다. 편의상 \(K_{a}=k\), 초기 몰수를 \(m_{i}\)라고 하면, 위 예제와 비슷한 상황의 산-염기 문제에서는 다음과 같은 식을 얻는다. \[\frac{\left(a_{n+1}\right)^{2}}{m_{i}-a_{n}}=k\] 따라서 이 식을 넘기면 \(f(x)\)를 얻는다. \[f(x)=\sqrt{k\left(M_{i}-x\right)}\]

수열 \(a_{n}\)을 이렇게 정의했다면, 이 수열이 수렴한다는 가정 하에(수렴하지 않으면 계산의 의미가 없음. 수렴 여부는 보여야 하지만 화학 문제를 풀 때는 무의미) \(\lim\limits_{n \rightarrow \infty}a_{n}=\lim\limits_{n \rightarrow \infty}a_{n+1}\)이기 때문에 이 극한값을 \(\alpha\)라 하면 \(\alpha=f\left(\alpha\right)\)가 되어 \(y=f(x)\)와 \(y=x\)의 교점, 즉 방정식 \(f(x)=x\)의 해가 극한값이 된다. 이것이 지금 우리가 다루고 있는 산성 수용액의 pH를 구하는  문제에서는 \(\ce [H_{3}O^{+}]\)가 된다. 따라서 이 상황에서는 \(f(x)=\sqrt{k\left(M_{i}-x\right)}\)이기 때문에
\[f(x)=\sqrt{k\left(M_{i}-x\right)}=x\]인 \(x\)가 \(\ce [H_{3}O^{+}]\)이다.

이 방법이 왜 정확한 값을 구하는 것인지 생각 해 보자. 원래 우리가 풀어야 하는 이차방정식은 다음과 같다. \[\frac{x^{2}}{m_{i}-x}=k\] \[x^{2}-k\left(m_{i}-x\right)=0\] 이 방정식과 고정점 방법에서의 식을 비교할 수 있다. 어떤 \(x\)에서 시작하든 \(\lim\limits_{n \rightarrow \infty}a_{n}=\alpha\)라 하면 수열 \(a_{n}\)은 \(\alpha\)로 다가가는 수열이다. 고정점 방법에서도 \(\sqrt{k\left(M_{i}-x\right)}=x\)인 \(x\)가 \(\ce [H_{3}O^{+}]\)라고 했으므로 정확히 똑같은 방정식의 해가 되는 것이다.
여기서 핵심 개념은, 재귀함수 \(f(x)\)를 정의했을 때 이 재귀함수와 항등함수의 교점이 극한값이 된다는 것이다.

이때 우리는 '안정고정점'에 대한 논의가 필요한데, 가볍게 짚고 넘어 가겠다. 함수 \(f(x)\)와 \(y=x\) 의 교점 중 \(f'(a)<1\)인 점이 안정고정점이다. 어떤 고정점이 안정고정점이면 반드시 재귀함수로 이루어진 수열은 그 고정점으로 수렴하게 되어있다. 이때, 산 염기 문제에서는 \(-y\)방향으로 향하는 무리함수가 그려지기 때문에 반드시 \(f'(x)<0\)이다. 따라서 반드시 그 극한값은 정확히 이차방정식의 해가 된다.
위에 제시된 옥스토비 문제를 가지고 고정점 도형을 그려보았는데, 산-염기 문제 특성상 계수들이 엄청나게 작아 크게 확대한 모형을 첨부한다.

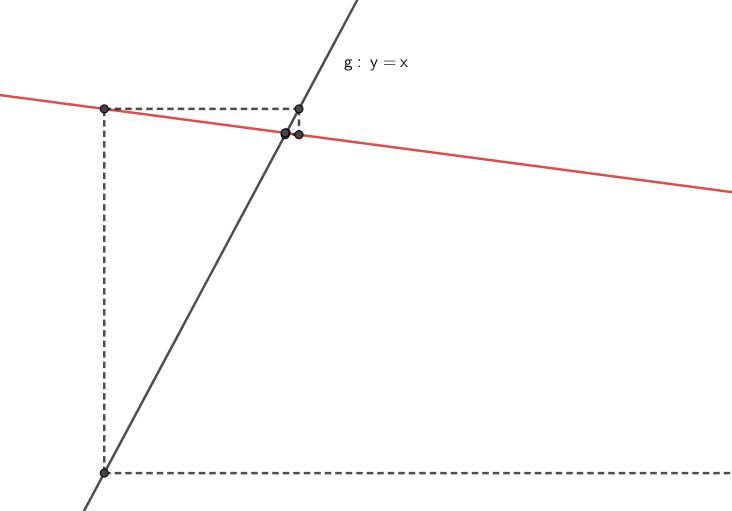
이렇게 화학에서 쓰이는 연속근사법에 대한 수학적 정당성을 보였다. 고정점 도형을 통해서 무리함수와 항등함수의 교점을 찾고 이것을 통해 pH를 구할 수 있게 되는 것이다. 연속 근사법의 설명 도중 '원하는 유효숫자 내에 들어올때 까지'라는 표현을 썼다. 왜냐하면 이 수열은 계속 고정점 도형 내에서 점점 수렴하는 직선들을 그리며 수렴값에 가까워지는 방향으로 진행하기 때문에 오차 값에 대한 수열을 정의하면 이 수열은 오차 값이 \(0\)으로 수렴하는 단조감소수열이다.

이때 이 오차수열이 \(0\)으로 수렴하는 속도는 함수 \(f(x)\)가 결정하고, 위의 Oxtoby 예제에서는 거의 두 번 만에 극한값과 매우 유사한 값을 가진다는 것을 알 수 있다.