수학적으로 전기력선 그리기
시작에 앞서, 물리(Physics)란, 정성적 예측 이후의 정량적 증명 - 혹은 정량적 계산 이후의 정성적 설명으로 이루어지는 학문이다. 우리가 물리를 대하는 자세는 정성과 정량이 조화를 이루고, 수학적 논리와 물리적 직관의 조화를 이루는 아름다운 균형을 유지해야 한다는 것을 잊지 말아야 한다.
이 탐구는 정성적 예측 - 정량적 검증 - 정성적 보완 순으로 이루어진다.
개요
이 탐구는 쌍극자의 전기력선/자기력선을 ‘stereographic projection’이라는 수학적 방법으로 그릴 수 있음을 제안한다. 구와 타원체를 \(xy\) 평면에 사영하여 쌍극자의 전기력선과 자기력선을 그릴 수 있음을 첫 추측에 두고 출발하였다. 이 탐구에서 다루는 것은 쌍극자의 전기력선/자기력선 밖에 없으므로 이 말은 ‘전기력선‘이라고 간소화하여 다루겠다.
Stereographic projection(평사도법)
링크 13분 부근을 보면, stereographic projection의 그래픽이 나온다. \(R^{3}\)의 구(Riemann sphere)을 \(R^{2}\)에 사영하는 것이다.
사영기하학을 기반으로 한 1 on 1 function의 일종, 복소해석학까지 확장 가능한 analytic function이다. 이때 analytic function(해석함수)는 복소해석학에서 ‘각을 보존하는 변환: 등각사상(conformal mapping)’으로 이해하는 것이 이 탐구 주제에서 가장 적절하다. 3차원 입체도형을 2차원 평면에 사영하는 것으로, 북극(north pole)과 입체도형의 각 점을 잇는 직선이 평면과 만나는 지점을 입체도형의 각 점과 일대일 대응시키는 사상(mapping)을 stereographic projection이라고 한다.
전기력선을 물리적으로 그리기
전기력선을 물리적으로 그리는 것은 너무나 간단하다. \(\vec{E}=-\nabla{V}\)이기 때문에, 전위 함수를 설정하고 그래디언트를 취해준 뒤, -부호를 붙여주고 그 그래프(vector field의 flow, 아니면 vector field 그 자체)를 그려준다면 끝이다. 임의의 점에서 전기장을 그릴 때, 쌍극자의 거리로부터 역제곱에 비례하는 크기로, 두 벡터를 빼주어 생긴 벡터가 그 점에서의 전기장 벡터가 되고, 그 모든 점을 2차원평면에서 그린 것이 전기장의 vector field가 되는 것은 너무나도 자명한 사실이다. 그려보면 다음과 같다.
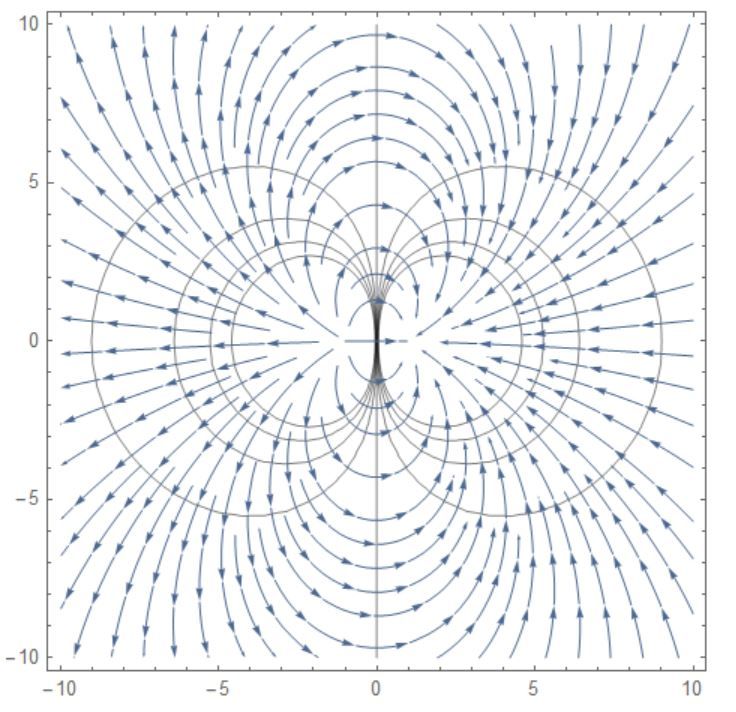
전기력선을 수학적으로 그리기
*추측의 근거: 정성적 예측
전기력선과 등전위선의 모양이 구를\(xy\)평면에 사영한 것과 매우 닮았다는 것에서 기초하였지만, 그저 닮았다는 것만으로는 정성적 해석과 예측이 너무 부족하다. 따라서 다음의 근거들로 유사하다는 것을 예측했다.
1. 전기력선은 \(+q\)에서 \(-q\)로 가는 모든 경로들을 그린 곡선인데, 구의 양 꼭짓점으로 가는 모든 경로, 즉 대원(great circle)을 그린 것이 사영하면 전기력선이 된다.
2. 등전위선은 전기력선과 반드시 수직인데, 그것이 구와 타원체에서 한 꼭짓점에서 다른 꼭짓점까지 가는 대원들과 수직인 가로로 입체도형을 두르는 폐곡선들, 즉 원과 타원이 입체도형 내에서 수직이기 때문에, conformal mapping인 stereographic projection에서 각을 보존하여 \(xy\)평면에서도 수직인 것이다.
3-a. conjecture 1: 구를 사영하여 전기력선을 그릴 수 있다. (실패)
처음 conjecture가 구를 향했던 것은, 처음 이 conjecture를 세우게 된 계기가 구의 stereographic projection이며, 매우 모양이 유사하기 때문이다. 그러나 결과적으로, 구를 사영한다고 해서 전기력선을 그릴 수 있는 것이 아니다. 이에 대한 탐구 과정은 아래와 같다.
- \((-1,0)\)에 \(+4\pi\epsilon_{0}\)의 전하를 띤 입자가, \((1,0)\) \(-4\pi\epsilon_{0}\)의 전하를 가진 입자가 놓여 있다.
- 구를 \(\theta,\phi\)로 매개화한다. \[\begin{bmatrix}x\\y \\z \end{bmatrix}=\begin{bmatrix}\sin\theta\cos\phi\\\sin\theta\sin\phi \\\cos\theta \end{bmatrix}, (0\leq\theta\leq\pi,0\leq\phi\leq 2\pi)\]
- 구를 \(x\)축을 기준으로 \(t\)만큼 회전한 행렬을 곱해준다. 구를 회전하는 이유는 쌍극자 간의 거리를 조절하는 방법이 구를 사영할 때는 구를 기울이는 것 외에 존재하지 않기 때문이다. \((0,0,1)\)에서 사영하기 때문에 구의 반지름을 조절하는 것은 제외하였다.
- 회전행렬을 곱해주면 다음과 같다. \[\begin{bmatrix}1&0&0\\0&\cos t&\ -\sin t \\0&\sin t& \cos t\end{bmatrix}\begin{bmatrix}\sin\theta\cos\phi\\\sin\theta\sin\phi \\cos\theta \end{bmatrix}=\begin{bmatrix}\sin\theta\cos\phi\\\cos t\sin\theta\sin\phi-\sin t\cos\theta \\\sin t\sin\theta\sin\phi+\cos t\cos\theta \end{bmatrix}\]
- stereographic projection의 행렬을 \(A\)라 하면, \(A\)는 다음과 같다. \[\begin{bmatrix}\frac{x}{1-z} \\\frac{y}{1-z}\\0 \end{bmatrix}=A\begin{bmatrix}x \\y\\z \end{bmatrix}\]
- 회전한 구에 stereographic projection 변환을 취해주면, 즉 행렬\(A\)를 곱해주면 다음과 같다. \[A\begin{bmatrix}\sin\theta\cos\phi\\\cos t\sin\theta\sin\phi-\sin t\cos\theta \\\sin t\sin\theta\sin\phi+\cos t\cos\theta \end{bmatrix}=\begin{bmatrix}\frac{\sin\theta\cos\phi}{1-\left(\sin t\sin\theta\sin\phi+\cos t\cos\theta\right)}\\\frac{\cos t\sin\theta\sin\phi-\sin t\cos\theta}{1-\left(\sin t\sin\theta\sin\phi+\cos t\cos\theta\right)} \\0\end{bmatrix}\]
이것이 구를 \(xy\)평면에 사영한 매개곡면이다. 이 중 대원(great circle)과 그에 수직인 원들을 택하여 GeoGebra에서 ‘수열‘ 명령어로 처리한 후, \(\theta,\phi\)중 한 변수에 대한 매개곡선을 만들어 전기력선과 등전위선을 그릴 수 있다. 이때, 전기력선은 회전구의 북극에서 남극으로 가는 모든 길이기 때문에, \(\phi=\frac{2 k\pi}{n}\)으로 고정하고, \(\theta\)에 따른 매개곡선들의 \(k\)에 대한 수열로 그린다. 등전위선은 반대로 \(\phi\)에 대한 매개곡선이므로, \(\theta=\frac{k\pi}{n}\)으로 고정하고 \(\phi\)에 따른 매개곡선들의 \(k\)에 대한 수열로 그린다.



conjecture 1의 실패: jacobian multiplication을 통한 comparison
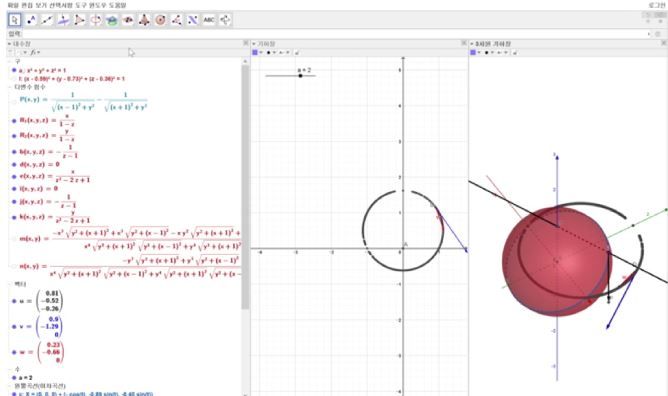
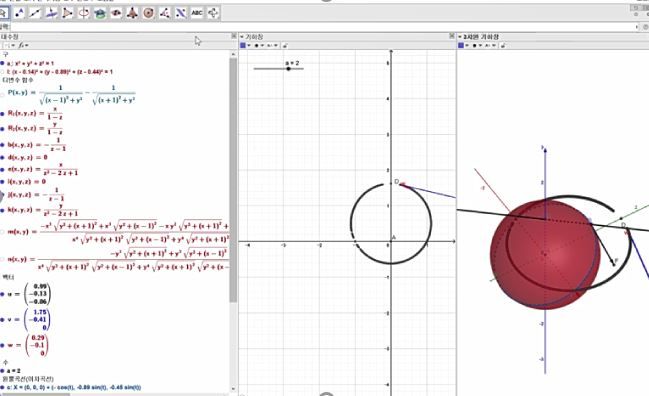
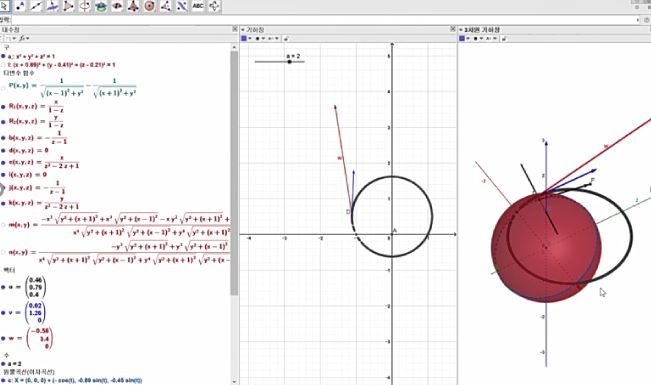
위 사진에서 볼 수 있듯이, GeoGebra를 통해서 구의 사영과 전기력선이 일치하지 않는다는 것을 확인했다.평면상에서의 임의의 점에서의 전기장 벡터와, 그에 상응하는 구의 점에서의 접벡터에 stereographic projection matrix의 jacobian을 곱해주어서 그 둘을 그려봤는데, 그림과 같이 달랐다. 따라서 구를 사영한다고 해서 전기력선을 얻는 것이 아니라는 결론을 얻었다.
3-b. conjecture 2: 타원체(ellipsoid)를 사영하여 전기력선을 그릴 수 있다.
구에서 일치하지 않았다. 그렇다면 매개화를 달리하여 타원의 북극에서 사영을 해보면 어떨까라는 의문을 가지고, 똑같은 방식으로 매개화 후 사영해보았는데, 이 역시 완벽하게 일치하지 않았다. 이때 타원체에서 쌍극자 간의 거리를 조절하는 방식에는 새로운 것이 하나 생겼는데, conjecture 1에서는 구의 각 축에 해당하는 반지름이 일정했기 때문에 구를 \(x\)축에 대하여 \(t\)만큼 회전하는 회전행렬을 곱해주는 방식이었지만, 타원체에서는 \(x\)축 방향의 반지름을 조절해주면 된다. (물론 구에서도 반지름을 조절할 수 있지만, 회전행렬에 의의를 둔다.)
타원체 역시 구와 완전히 동일한 방법을 적용하여 분석했지만, 이 역시 일치하지 않았다. 직관에 가장 가까웠던 구와 타원체가 정량적으로 일치하지 않고, 근사만 가능하다는 것을 통해서 정량적인 접근 이외에 어떤 정성적 분석을 통해 왜 직관과 맞지 않는지에 대한 해석이 필요했다. 그것은 바로 stereographic projection의 ‘conformal mapping’으로서의 성질에만 주목했지, 더 나아가 도형을 보존하는 성질까지 생각하지 못한 것이다. 구의 단면은 반드시 원이며, 타원체를 두르는 곡선은 반드시 타원이다. 이때, 구와 타원체를 두르는 곡선들을stereographic projection을 통해 \(R^{2}\)에 사영시킨 도형은 원과 타원이 된다. 그런데 전기력선과 등전위선은 원호, 원, 타원의 어떤 도형도 아니다. 이를 수학적으로 분석해 보았을 때, 절대 구와 타원체를 사영하여 전기력선을 얻을 수 없고, 다른 도형이어야 한다는 것을 알 수 있다. 하지만 그 차이가 매우 근소해 쉽게 자기력선을 그리기 위해서 근사법을 사용할 수는 있다.
타원체를 매개화하면 다음과 같다. \[\begin{bmatrix}x\\y \\z \end{bmatrix}=\begin{bmatrix}a\sin\theta\cos\phi\\b\sin\theta\sin\phi \\c\cos\theta \end{bmatrix}, (0\leq\theta\leq\pi,0\leq\phi\leq 2\pi)\]
이때 \(a,b,c\)는 각 축 방향 반지름이 된다. 아래 그림은 \(a,b,c\) 의 값에 따라 전기력선과 등전위선을 그린 그림이다. 이때 각 축의 반지름으로 압축율과 쌍극자 간의 거리를 조절할 수 있다. 타원체를 사영할 때는 회전각 \(t\)를 직각(\(\frac{\pi}{2}\))으로 고정하고, 압축율과 거리를 조절한다. 이때 conjecture 1에서 했던 것처럼 타원체의 \(xy\) 평면에 대한 사영을 계산하면 다음과 같다.
(\(A\)는 stereogrpahic projection matrix) \[A\begin{bmatrix}1&0&0\\0&\cos\frac{\pi}{2}&-\sin\frac{\pi}{2} \\0&\sin\frac{\pi}{2}&\cos\frac{\pi}{2} \end{bmatrix}\begin{bmatrix}a\sin\theta\cos\phi\\b\sin\theta\sin\phi \\c\cos\theta \end{bmatrix}=A\begin{bmatrix}a\sin\theta\cos\phi\\-c\cos\theta \\b\sin\theta\sin\phi \end{bmatrix}=\begin{bmatrix}\frac{a\sin\theta\cos\phi}{1-b\sin\theta\sin\phi}\\\frac{-c\cos\theta}{1-b\sin\theta\sin\phi} \\0\end{bmatrix}\]
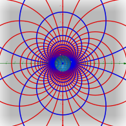
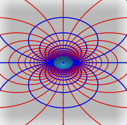
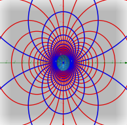
3-c. conjecture 3: 전기력선/등전위선이 이루는 도형을 3차원 상에 쌓은 후 사영
결국 원과 타원 모두 도형을 보존하는 mapping인 stereographic projection을 통해 전기력선으로 나타날 수 없음을 알았다.
이때 쌍극자의 전위를 살펴보자. 전하량의 크기가 \(4\pi\epsilon_{0}\)이고, \((-1,0)\),\((1,0)\)에 각각 양전하와 음전하가 놓인 전위 함수는 다음과 같다.\[V(x,y)=\frac{1}{\sqrt{\left(x+1\right)^{2}+y^{2}}}-\frac{1}{\sqrt{\left(x-1\right)^{2}+y^{2}}}\] 위의 wolfram에서 전기력선을 그릴 때 이와 같은 함수를 사용했다. 이때 등전위선은 전위함수의 스칼라 값이 일정한 곡선을 의미한다.
이때, 이것을 수학적으로 해석하면 두 점(이 상황에서는 \((-1,0)\),\((1,0)\) 으로부터 거리의 역수의 차가 일정한 곡선이 된다. 이 곡선을 편하게 ‘등전위선’이라고 정의하고, 등전위선을 3차원 공간에 \(yz\)평면과 나란하게 쌓고, \(x\)축을 따라서 등전위선들과 수직인 곡선들로 가로 방향을 만들면 등전위선과 전기력선이 모여 만든 3차원 도형을 얻을 수 있다. 이 모델이 전기 쌍극자의 퍼텐셜과 전기장을 3차원 riemann sphere안에 압축해 놓은 것이 된다. 이때, 3차원 riemann sphere \(S^{3}\)는 \(R^{2}\), 즉 \(xy\)평면의 점 개수보다 한 개 많다. 왜냐하면 \(S^{3}=R^{2}\cup\left\{\infty\right\}\)이기 때문이다. ‘무한’에 해당하는 점은 stereographic projection의 시작점이 되는 ‘북극‘이다.
정리 및 요약
자기력선과 전기력선의 모양이 구를 stereographic projection을 한 모습과 매우 유사하여 연구를 시작하게 되었다. 구와 타원체를 사영시켜 전기력선을 만들 수 있다는 두 conjecture가 완전히 불일치하다는 것이 증명되었지만, 결국 ‘거리의 역수의 차가 같은 곡선’을 ‘등전위선’이라 정의하여 3차원 상에서 등전위선을 매개화하고 이를 \(xy\)평면상에 사영한다면 이 방법으로 전기력선을 그릴 수 있다는 것을 알 수 있다. 등전위선이 수학에서 어떤 특별한 성질을 가진다거나, 곡선으로서 큰 특징을 가지는 곡선이 아니기 때문에 주요한 입체도형으로서 stereographic projection에 적용되지는 않는다. 하지만 구와 타원체로 매우 근접하게, 매우 낮은 오차로 전기력선의 vector flow curve와 contour line을 그릴 수 있다.
참고 문헌
[1]하나고등학교 탐구수학 3,4기 방과후 프린트물, 박성훈/이은창 선생님, 2018.
[2]기초전자기학(4th edition), David.J.griffiths, 2014.
