[혼돈 이론 #2] Lyapunov 지수를 이용한 혼돈의 확인

혼돈이란?

Chaos (혼돈) 은 초기 조건에 예민하게 의존하여,  계에 대한 예측이 불확실성을 띄는 경우를 말한다. 가장 많이 알려진 것으로는 나비 효과가 있다. 공중을 천천히 나는 나비가 공기흐름에 미세한 영향을 줘서 다음 주의 기후 상태를 예측하기 어렵게 된다 라는 말을 들어봤을 것이다. 아주 작은 초기 상태의 차이가 시간이 갈수록 점점 거대한 차이로 나타나는 특성을 설명한다. 이렇듯 초기 조건의 예민한 의존도 때문에 시간 변화에 따른 궤도가 매우 복잡해 보이게 된다. 또한 이러한 특징 때문에 초기 오차의 지수적 증가가 결국 측정 결과를 예측하기 어렵게 되는, 불확실성을 만들어 낸다.

Lyapunov 지수

혼돈 현상에 의한 초기 조건의 예민한 의존도를 정량적으로 표현하는 한 가지 유명한 방법이 있다. 바로, 러시아의 수학자 Lyapunov가 만든 리아푸노프 특정 지수(Lyapunov characteristic exponent)이다.

어떠한 계에 대한 리아푸노프 지수는 변수만큼 존재하게 된다. 우선은 하나의 변수에 대한 리아푸노프 지수를 표현해보자.

두 개의 초기 상태를 가진 계가 존재할 때, 초기 상태를 \(x_0\) 와 \(x_0+\epsilon\)이라고 하자. 그리고 이 두 개의 초기값으로부터 n번 되풀이한 뒤 얻어지는 값을 \(x_n\)으로 하자. Lyapunov 지수 \(\lambda\)는 2개 상태 간의 단위시간당 평균 지수적 증가 계수를 나타낸다. n번 되풀이 후 2개 \(x_n\) 값 사이의 차 \(d_n\)은 근사적으로 다음과 같다.

\[ d_n=\epsilon e^{n\lambda} \]

\(\lambda\)값이 음수이면 2개의 궤도는 수렴하게 되고, 0이면 유지,궤도는 발산하게 되어 혼돈이 발생된다.

이제 가장 간단한 1차원 맵에서의 Lyapunov 지수를 표현해보자. 저번 기사의 주제였던 로지스틱 맵에 대해 읽어봤다면, 여기서의 1차원 맵이 로지스틱 맵의 형태였다는 것을 알 것이다.

\[ x_{n+1}=f(x_n)\]

초기 상태 간의 차는 \(d_0=\epsilon\)이고, 한 번 되풀이된 후의 차이는 \(d_1=f(x_0+\epsilon)-f(x_0)\cong\epsilon\frac{df}{dx}\left|\begin{matrix}\\x_0\\\end{matrix}\right.\) 이다. \(\epsilon\)값이 매우 작기 때문에 미분꼴로 근사할 수 있다.

또한 n번 되풀이된 후의 차이 \(d_n\)은 다음과 같다. \(f(x)\)의 n번째 되풀이를 첨자 n을 붙여서 표시하였다.

\[d_n=f^n(x_0+\epsilon)-f^n(x_0)=\epsilon e^{n\lambda}\]

이를 정리하면, 다음과 같다.

\[\ln{\frac{f^n(x_0+\epsilon)-f^n(x_0)}{\epsilon}}=\ln{e^{n\lambda}}=n\lambda\]

\[ \lambda=\frac{1}{n} \ln{ \frac{f^n(x+\epsilon)-f^n(x_0) }{\epsilon} }=\frac{1}{n} \ln{\left| \frac{df^n(x)}{dx} \left|{\atop x_0}\right. \right|} \]

\(f^n(x_0)\) 값은 \(f(x_0)\) 값을 n번 되풀이한 것이므로,

\[ f^{n}(x_0) =f( f( \cdots (f(x_0)) \cdots ))  \]

n번째 되풀이에 관한 체인 룰을 사용하여 위의 식을 정리하자.

\[ \frac{df^n(x)}{dx} \left|{\atop x_0}\right.=\frac{df}{dx} \left|{\atop x_{n-1}}\right.\frac{df}{dx} \left|{\atop x_{n-2}}\right.\cdots \frac{df}{dx} \left|{\atop x_{0}}\right. \]

n을 무한대로 보내서 구하는 Lyapunov 지수를 maximal Lyapunov exponent라고 한다. 전체적인 궤도의 변화를 알아보기 위하여 반복 횟수를 늘리는 것이다. 이를 나타내보자.

\( n \rightarrow\infty \) 극한을 취하면,

\[ \lambda=\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{i=0}^{n-1}\ln\left|\frac{df(x_i)}{dx}\right|. \]

위와 같은 값을 얻을 수 있다.

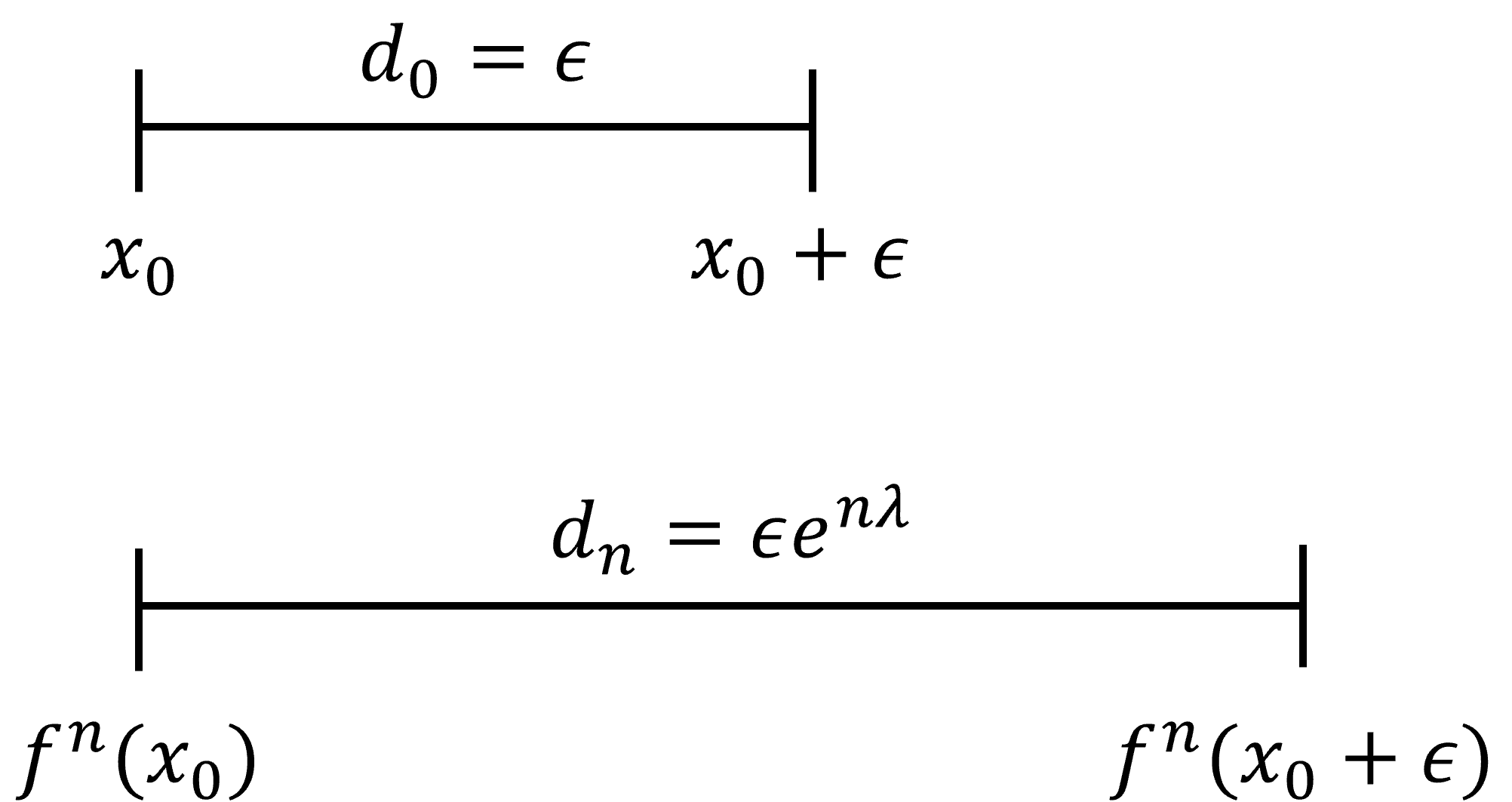
위에선 가장 간단한 1차원 맵에서의 Lyapunov 지수를 다뤘다. 이러한 이산적인 경우(맵이나 고정 지점 반복)가 아닌 연속적인 경우에서의 Lyapunov 지수를 표현해보자.

위에서와 마찬가지로 우선, 초기 상태의 차이를 나타내는 벡터 \(\delta \bold{Z}_0\) 를 정의한다.

시간 진행에 따라(이산적인 경우에서의 되풀이 과정에 대응되는 과정이다), 이 차이는 Lyapunov 지수 \(\lambda\)를 이용하여 근사적으로 다음과 같이 나타낼 수 있다.

\[ |\delta{\bold{Z}}(t)|\approx e^{\lambda t}|\delta{\bold{Z}}_0| \]

그리고 n번 되풀이를 무한 번 진행하는 것처럼 시간을 무한대로 보내면 \(t\rightarrow\infty\), 다음과 같다.

\[ \lambda=\lim_{t\rightarrow\infty}\ \lim_{\left|\delta {\bold{Z}_0}\right|\rightarrow0}\frac{1}{t}\ln{\frac{|\delta{\bold{Z}}(t)|}{|\delta{\bold{Z}}_0|}} \]

참고문헌

[1] Stephen T.Thornton & Jerry B. Marion, “4.7 Mapping,” in Classical dynamics of particles and systems, 5th ed., Seoul, Korea: Cengage Learning Korea Ltd., 2012, pp. 189-192.

[2] Wikipedia (2021, June 12). Lyapunov exponent [Online]. Available: https://en.wikipedia.org/wiki/Lyapunov_exponent#cite_note-cencini-1