[혼돈 이론 #3] Logistic Map의 Lyapunov 지수 확인하기

혼돈 이론 #1에서는 Logistic Map이 무엇인지, 그리고 혼돈 이론 #2에서는 Lyapunov 지수에 대해 알아보았다. 이번 글에서는 Logistic Map에 Lyapunov 지수를 적용하여 혼돈을 직접 확인해보려고 한다.

서론

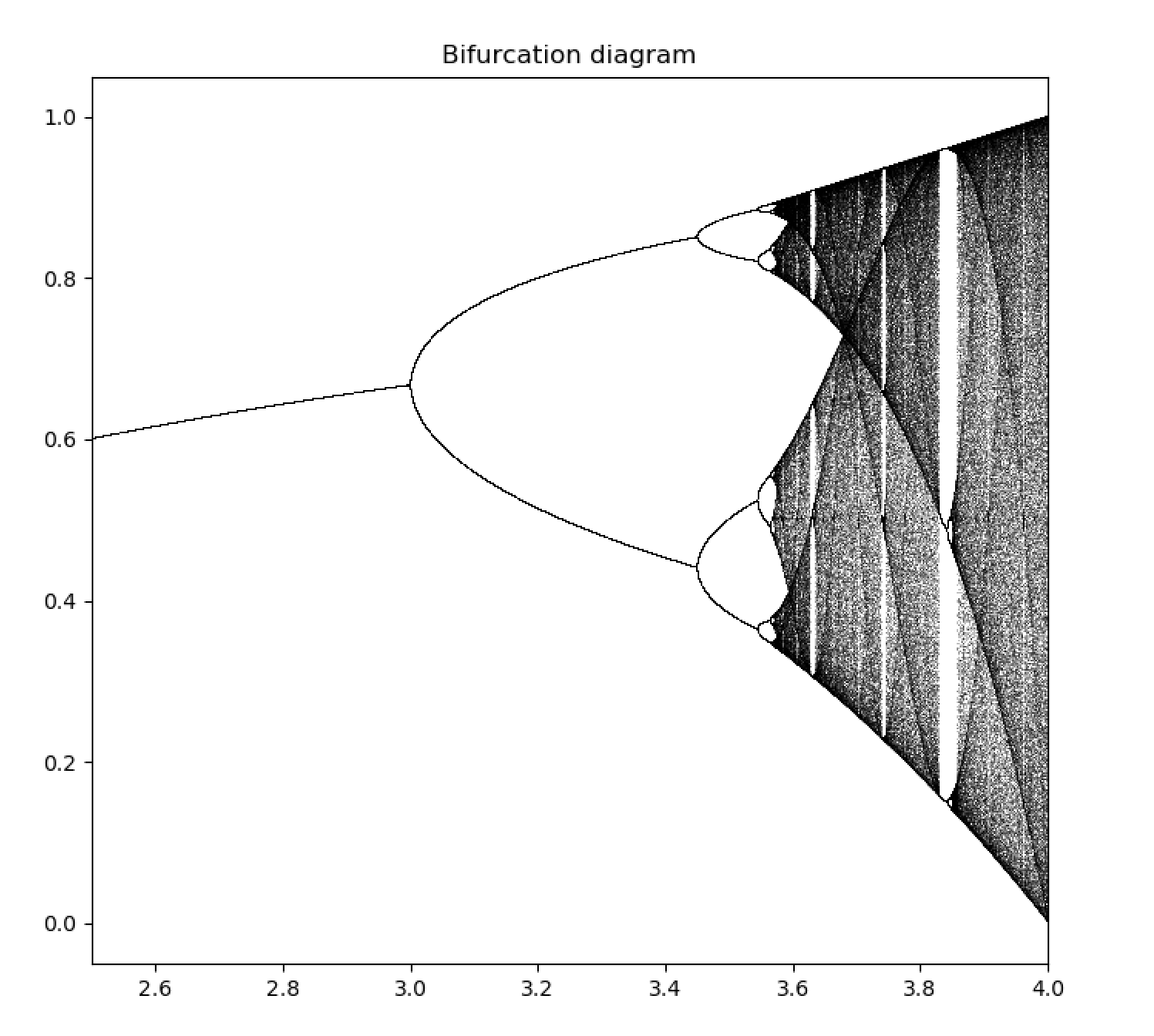
Logistic Map의 Bifurcation Diagram을 다시 상기해보자.  

\[f(α,x)=αx(1-x)\]

매개변수 \(\alpha \)에 따라 이산적인 행태를 보였던 것을 기억할 것이다.

\( \alpha \) 값이 커질수록 아주 조그마한 \( \alpha \) 값의 차이에도 두 궤적에 큰 차이가 발생하는 카오스가 나타났었다. 이 초기조건에 대한 민감성을 Lyapunov 지수를 이용하여 표현해보자.

Logistic Map에서의 Lyapunov 지수

혼돈 이론 #2에서 증명해 얻었던 1차원 맵에서의 maximal Lyapunov exponent는 다음과 같았다.

\[ \lambda=\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{i=0}^{n-1}\ln\left|\frac{df(x_i)}{dx}\right|. \]

이를 Logistic Map에 대입하자.

\[ f'(x_i)=\alpha - 2\alpha x_i\] 이므로, 다음과 같다.

\[ \lambda= \lim_{n\rightarrow\infty}\frac{1}{n}\sum_{i=0}^{n-1}\ln{\mid\alpha-2\alpha x_i\mid} \]

따라서 각각의 되풀이 과정에 대하여 더하여 평균 값을 취한다고 생각하면 된다.

매개변수 \( \alpha \)에 대한 Lyapunov 지수

이렇게 구한 각 \( \alpha \) 에 대한 Lyapunov 지수를 나타내면 다음과 같다.

(python 코드 참고 [2])

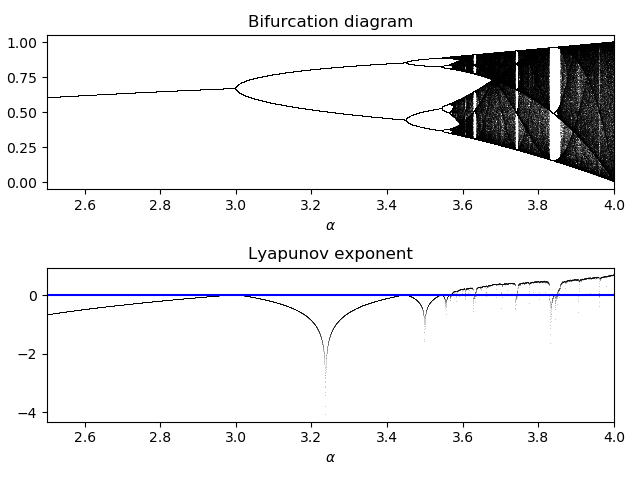
Lyapunov 지수를 통해 혼돈을 정량적으로 확인할 수 있다는 말의 의미를 이제 알 수 있을 것이다. 수렴구간, 즉 주기구간에서 Lyapunov 지수는 음수의 값을 가진다. 카오스 구간에서는 양수의 값을 가지는 것을 볼 수 있다. 또한 분기가 일어날 때 \( \lambda \) 값은 0이다.

\(f'(x)=0\)에서 안정점이 나타나게 되며 따라서 이 경우에는 \( \lambda=-\infty \)가 된다.

결론

이렇게 Logistic Map의 카오스적 성질을 Lyapunov 지수를 이용하여 확인해보았다. Logistic Map은 가장 간단한 형태의 1차원 맵 중 하나이다. 하지만 Lyapunov 지수는 n차원 맵에 대해서도 적용할 수 있다는 것을 기억하자. n차원이면 n개의 Lyapunov 지수가 존재하게 된다. 이러한 경우 혼돈이 일어나려면 여러 개의 지수 중 하나만 양수이어야 한다.

참고문헌

[1] Stephen T.Thornton & Jerry B. Marion, “4.7 Mapping,” in Classical dynamics of particles and systems, 5th ed., Seoul, Korea: Cengage Learning Korea Ltd., 2012, pp. 189-192.

[2] 죠옹. (2021, July 7).  리아프노프 지수 - 로지스틱 맵 [Online]. Available:https://mons1220.tistory.com/174