물리학에서 운동방정식은 질점의 운동을 설명하며, 다음과 같이 표현할 수 있다.\[\ddot{x} = F(\dot{x}, x, t)\]

이는 2계 미분방정식으로, 시간에 따른 물체의 운동은 곧 \(x(t)\)를 의미하여 이를 구하기 위해서는 미분방정식의 해를 구해야 한다. 본 글에서는 예시로 계수를 고려하지 않은 강제진동자 (Driven Oscillator)의 다음 운동방정식을 살펴보려 한다.\[\ddot{x} + \dot{x} + x  = \sin{t}\]이때, 이 식은 2계 1차 비동차 상미분방정식이다.

Euler 방법

\(y\)에 대해 \[\textrm{d}{y} / \textrm{d}{t} = f(t,y)\]라 하자. 이때, \[y_{n+1} = y_n + h f(t_n, y_n)\]로 근사가 가능하고, 이를 Euler 방법이라 한다.

이는 \(y\)의 테일러 전개 \[y(t_0 + h) = y(t_0) + h\dot{y}(t_0) + \frac{1}{2} h^2 \ddot{y}(t_0) + \mathcal{O}(h ^3)\]\[t_{n+1} = t_n + h\]

에서 2차 이상의 항을 무시하여 유도할 수 있다. 곧, 오일러 방법은 1차항만 고려한 근사이다. 이로 인해 오일러 방법은 상당한 오차가 발생하고, 이를 해결하기 위해서는 고차항도 고려해야 한다.

Runge-Kutta 방법

Runge-Kutta 방법은 Euler 방법의 일반화로, 다양한 차수의 근사가 존재한다. 그 중 가장 많이 사용되는 방법은 RK4, 곧 4차 Runge-Kutta 방법이다.

위와 같은 \(f\)와 \(y\)에 대해,\[\begin{aligned} k_1 &= f(t_n,  y_n), \\ k_2 &= f(t_n + h/2, y_n + h k_1 / 2), \\ k_3 &= f(t_n + h/2, y_n + h k_2 / 2), \\ k_4 &= f(t_n + h, y_n + h k_3)\end{aligned} \]를 정의하자. 이때,\[y_{n+1} = y_n + \frac{1}{6} h (k_1 + 2k_2 + 2k_3 + k_4)\]\[t_{n+1} = t_n + h\]

로 근사가 가능하고, 이것이 RK4이다. 이 근사의 유도는 테일러 전개를 통해 가능하다.

운동방정식의 풀이

위에서 설명한 Euler 방법과 Runge-Kutta 방법은 1계 미분방정식에 대해서만 적용이 가능하지만, 운동방정식은 2계 미분방정식이다. 운동방정식에 Runge-Kutta 방법에 적용하기 위해서는 추가적인 변형이 필요하다.

\(\ddot{x} + \dot{x} + x  = \sin{t}\)에서, \(u \coloneqq \dot{x}\), \(v \coloneqq x\)로 정의하자. 이때 운동방정식을 다시 나타내면,\[\dot{u} + u + v = \sin{t}\]이고, 곧\[\dot{u} = \sin{t} - u - v,\quad\dot{v} = u\]이다.

이를 다시 나타내면, \[\dot{u} = f(u, v, t), \quad \dot{v} = g(u, v, t)\]의 꼴로, 이는 Runge-Kutta 방법을 2번 적용하여 해를 구할 수 있는 형태이다. 이를 python 코드로 나타내면 다음과 같다.

from numpy import sin, arange

h = 0.01

def rk4(f, t, u, v):
    k1 = f(t, u, v)
    k2 = f(t + h/2, u + h * k1 / 2, v + h * k1 / 2)
    k3 = f(t + h/2, u + h * k2 / 2, v + h * k2 / 2)
    k4 = f(t + h, u + h * k3, v + h * k3)
    
    return u + h * (k1 + 2 * k2 + 2 * k3 + k4) / 6
    
for t in arange(0, 1, h):    
    vel_ = rk4(
              lambda t_, u, v,: sin(t_) - u - v,
              t, vel, pos
          )

    pos = rk4(
              lambda t_, v, u,: u,
              t, pos, vel
          )
  
    vel = vel_
    
    print(f"t={t}, x={pos}, x'={vel}")

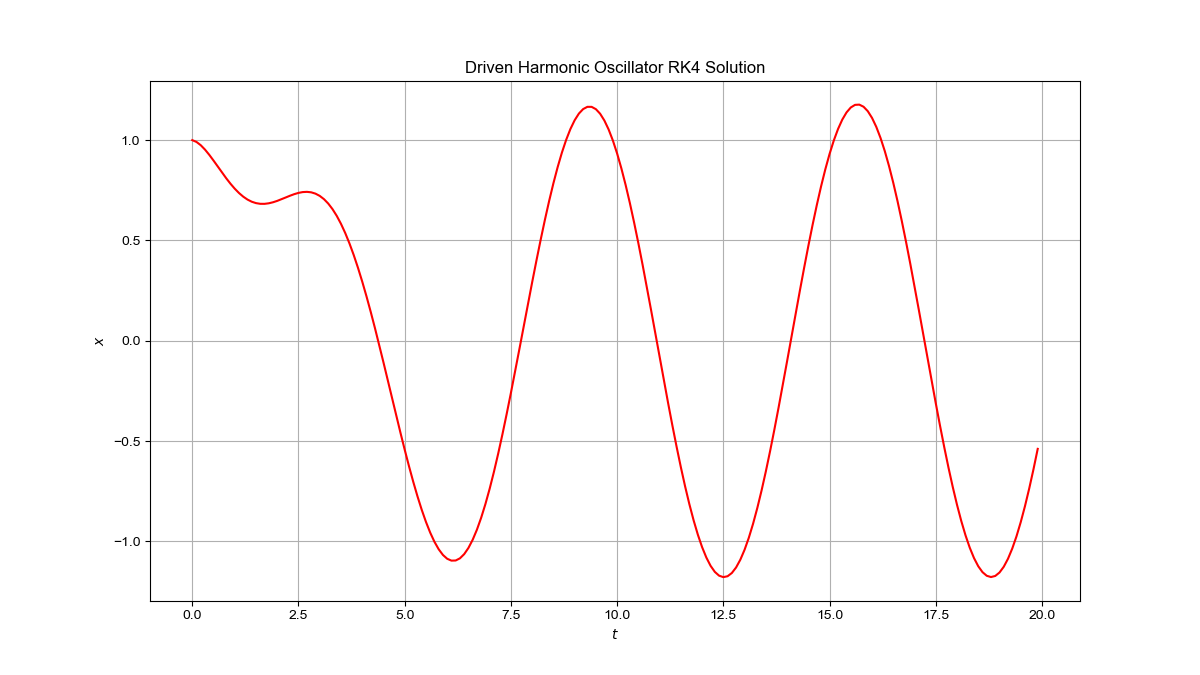
결과는 다음과 같다.