RhB를 통한 전형원소의 사중결합 가능성 확인

화학결합을 논할 때, 높은 결합 차수를 가지는 화합물들에 관한 이야기는 주로 전이금속의 영역이었다. 단순히 사중결합 이외에도, 오중, 육중결합 역시 전이금속끼리의 화학결합에서는 발견되었다. 그러나 2020년 1월, 브라운대학교의 라이 셩 왕 교수팀이 붕화로듐(\(\ce{RhB}\)) 분자가 사중결합을 한다는 연구결과를 발표하면서 전형원소의 고차 결합의 가능성을 제시하였다.

전이금속의 사중결합과 전형원소와의 차이점

기존에 사중결합을 한다는 것으로 알려져 있던 전이금속의 결합에 대한 설명은 델타(\(\delta\)) 결합을 통해 이루어졌다. 델타결합은 4개의 돌출부를 가진 오비탈, 즉 주로 \(d\) 오비탈끼리 겹치면서 형성되는 결합이다. 이를 기반으로 사중결합을 하는 경우 두 원자는 시그마(\(\sigma\)) 결합 한 개, 파이(\(\pi\)) 결합 두 개, 델타(\(\delta\)) 결합 한 개를 한다. 분자 오비탈 (Molecular Orbital, MO) 이론에 기반하여 설명을 하면, \(3d\) 오비탈끼리 결합을 하는 경우 \(\sigma_{3d}\), \(\pi_{3d}\) 결합성 궤도함수보다 높은 에너지 준위에 \(\delta_{3d}\) 궤도함수가 존재하여 8개의 전자가 각 궤도함수에 2개, 4개, 2개씩 들어가서 결합을 형성하게 된다. 이러한 결합을 하는 분자로는 \(\ce{Re2Cl8}\) 등이 있다.

그러나 전이금속과는 달리, 전형원소의 경우에는 4차 이상의 결합이 불가능하다고 알려져 있었다. 전형원소들은 \(s, p\) 오비탈의 전자를 원자가 전자로 가지는데, \(d\) 오비탈에 비해 \(s, p\) 오비탈은 더 짧고 굵은 모양을 가지고 있어서 전자가 더욱 비편재되어있고, 이 때문에 분자 내부 공간을 점유하는 전자의 밀도가 높아서 결합이 안정하지 못한 것이다. 그러나 오랜 기간동안 많은 사람들의 머릿속에 있던 이 생각이 라이 셩 왕 교수의 발견으로 변화를 맞이하게 되었다.

RhB의 발견

왕 교수팀은 \(\ce{RhB}\), 그리고 \(\ce{RhB(BO^-)}\)에 사중결합이 존재함을 밝혀냈다. 이 결합이 존재한다는 것을 예측할 수 있게 한 요인으로는 두 가지가 있었는데, 첫 번째는 광전자 분광(PES) 실험의 결과이다. 광전자 분광법은 높은 에너지의 전자기파를 시료에 비추었을 때 방출되는 광전자의 운동에너지를 측정하여 분자의 전자 구조를 파악하는 연구방법이다. 전자기파를 비추면, 분자의 가장 높은 에너지 준위의 분자오비탈에 존재하는 전자부터 방출되기 때문에 이 순서대로 기록된 그래프에는 여러 개의 피크가 존재하게 된다. 그리고 각각의 피크에서의 운동에너지 값과 초기 전자기파의 에너지의 차는 곧 방출된 전자가 들어 있던 오비탈의 결합에너지와 같다. 왕 교수팀은 \(\ce{RhB^{-}}\) 와 \(\ce{RhB(BO^{-})}\)에 대한 PES를 실험으로 측정하였다. 그런데 그림 1-(a)에서도 볼 수 있듯이, \(\ce{RhB(BO^{-})}\)에 대한 PES가 실험값과 이론값이 일치하지 않는 것을 확인할 수 있었다. 연구자들은 분자의 구조가 그림의 왼쪽 상단에 있는 것과 같은 선형 구조일 것이라고 예측하였고, 이를 기반으로 각 피크에서의 결합에너지를 계산하였지만 이는 측정값과 달랐다. 어떠한 새로운 형태의 구조, 결합이 존재한다는 것이었다.

두 번째는 결합 길이와 각도이다. PES 실험의 결과의 연장선에서 연구자들은 광학 분광법을 통해결합 길이와 각도를 측정하였다. 역시나 \(\ce{RhB(BO)}\)와 그 음이온은 조금 특별한 모습을 보였다. 그림 1-(b)의 오른쪽 두 분자의 그림에서 볼 수 있듯이, \(\ce{RhB(BO)}\)와 \(\ce{RhB(BO^{-})}\)는 굽은형 구조를 가지며, 중성분자에서의 결합각이 음이온보다 작았다. 또한 두 개의 \(\rm{Rh-B}\) 결합 길이가 눈에 띄게 차이 남을 알 수있다. 이러한 특이점들이 \(\rm{Rh-B}\) 사이에 세기가 강한 특이한 결합이 존재함을 예상해볼 수 있게 하였다.

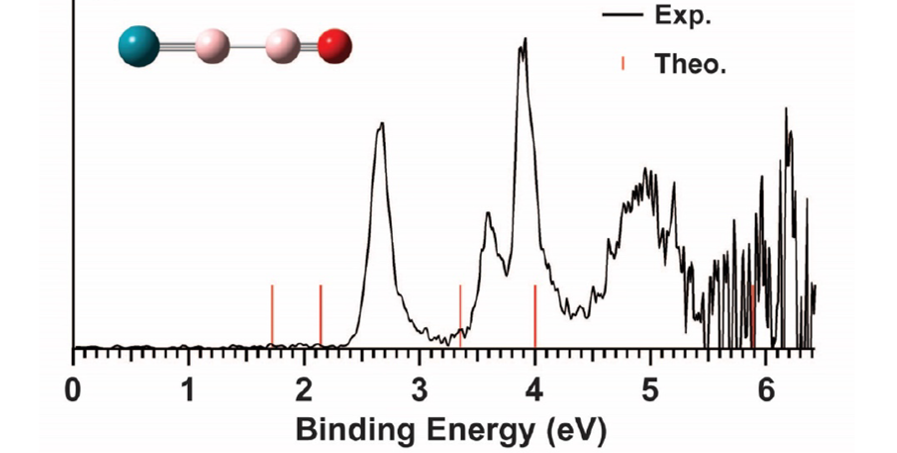
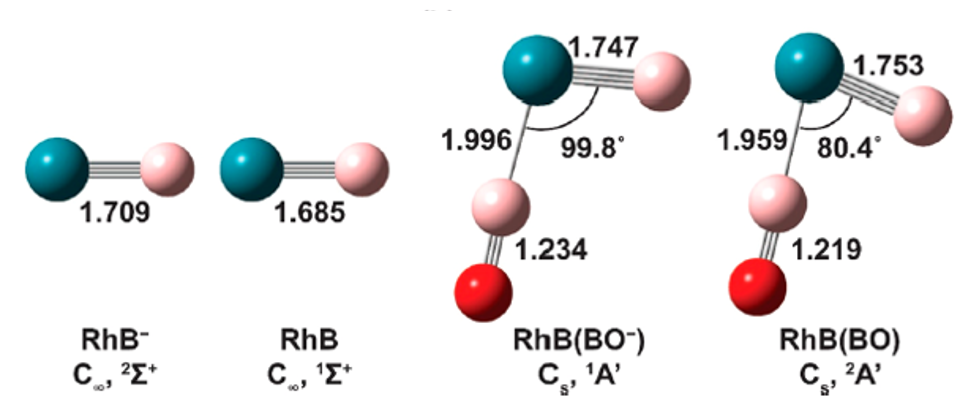
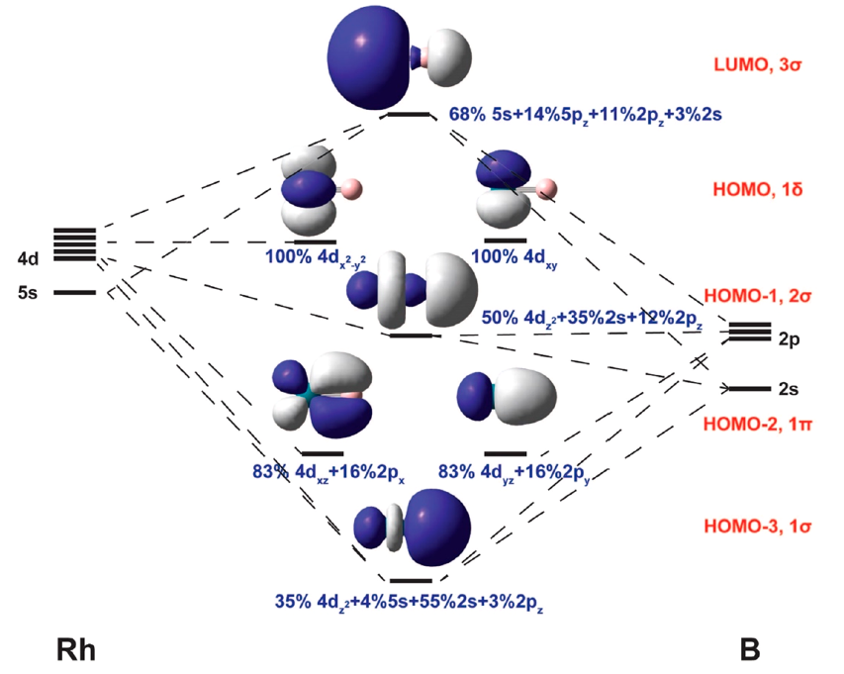
결국 그림 2와 같이 왕 교수팀은 \(\ce{Rh}\)와 \(\ce{B}\)의 결합에 관한 분자오비탈 모형을 그려낼 수 있었다. 이때 \(\ce{RhB}\)의 LUMO(가장 낮은 비점유된 분자오비탈)는 \(\ce{Rh}\)의 5s, 4d 오비탈과 B의 2s, 2p 오비탈 사이의반결합성 시그마(\(\sigma\)) 결합인데, 이것이 맞다는 것을 증명하는 데에 위에 언급된 PES가 이용될 수 있다. 연구자들이 측정한 \(\ce{RhB^{-}}\) 의 PES에서 첫 번째 피크에 해당하는 결합에너지가 0.961eV였다. \(\ce{RhB}\)가 \(\ce{RhB^{-}}\)가 될 때 전자는 \(\ce{RhB}\)의 LUMO에 들어가게 되는데, 따라서 첫 번째 피크의 결합에너지인 0.961eV는 \(\ce{RhB^{-}}\) 의 가장 높은 에너지 준위의 분자오비탈에서 방출되는 전자에 대한 결합에너지 값이므로, \(\ce{RhB}\)이 LUMO에 위치한 전자가 방출될 때의 에너지이다. 이론적으로 이 값을 계산했을 때 0.968eV가 나와, 실험값과 이론값이 상당히 비슷함을 알 수 있다. 또한 \(\rm{Rh-B}\)의 결합에 참여하는 분자오비탈은 총 4개로, 시그마(\(\sigma\)) 결합 2개와 파이(\(\pi\)) 결합 2개이고 각각의 MO에 전자가 2개씩 들어간다. 모두 결합성분자오비탈에 속하므로, 결합의 차수는 4.0이 된다. 이로써 전형원소인 \(\ce{B}\)도 사중결합을 함이 확인되었다.

참고 문헌

[1] Cheung, L., Chen, T., Kocheril, G., Chen, W.-J., Czekner, J., & Wang, L.-S. (2020, 01). Observation of Fourfold Boron-Metal Bonds in RhB(BO–) and RhB. The Journal of Physical Chemistry Letters, 11 (3), 659-663.
[2] Jensen, W. (2013, 06). The Origin of the Sigma, Pi, Delta Notation for Chemical Bonds. Journal of Chemical Education, 90 (3), 802-803.
[3] Nguyen, T., Sutton, A., Brynda, M., Fettinger, J., Long, G., & Power, P. (2005, 12). Synthesis of a Stable Compound with Fivefold Bonding Between Two Chromium(I) Centers. Science (New York, N.Y.), 310 (5749), 844-847.
[4] Oxtoby, D. W., Gillis, H. P., & Campion, A. (2012). Principles of modern chemistry (7th ed.). Cengage.
Cover Image from https://www.yu.edu/sites/default/files/ThinkstockPhotos-658148844.jpg