수면 각성 제어의 수학적 모델링 3편 - 수면 각성 모델링의 현주소

앞서 작성한 두 개의 글에서 수면-각성 제어, 그리고 렘수면 제어와 관련된 수학적 모델링에 대해 살펴보았다. Two-process model과 Sleep-wake flip-flop model을 통해 인간이 잠 들고 깨어나는 현상을 수학적으로 표현하여 설명할 수 있었다. 또, Reciprocal interaction model에서는 렘수면을 유도하는 신경그룹과, 렘수면을 억제하여 비렘수면을 유도하는 신경그룹 간의 상호작용을 수학적으로 표현하여, 수면 중에 렘수면이 주기적으로 발현되는 현상을 수식화할 수 있었다.

그러나 단순한 수학식 몇 개로 복잡한 생체 현상인 수면과 각성, 꿈꾸는 과정(렘수면) 등을 모두 표현하는 것은 쉽지 않은 일이다. 인체는 로봇이나 컴퓨터가 아닌 생물체이기 때문에 논리 법칙과 이론적인 알고리즘만으로 설명할 수 없는 부분이 매우 많다.

필자는 이 분야에 대한 호기심으로 여러 자료를 찾아가며 그동안 알게 된 지식들을 이곳에 정리해보았다. 그러나 수면의 수학적 모델링에 대해 알아볼수록, 소수의 학자들만 관심을 가지는 전문적인 분야다보니, 다양한 자료를 확보하는 것이 쉽지 않았다. 앞서 작성한 두 개의 글에서는 개념적으로 설명 가능한 범위에서 수면 현상을 수학적으로 풀어내는 것이 가능했지만 본 글에서 소개할 내용은, 여러 수면 현상과 과정들이 얽혀있는 것을 현상학적으로 기술한 식이 많기 때문에 각 수식의 수학적인 유도 과정을 설명하지 못한 경우가 많다. 그러므로 최대한 쉽게 개념을 설명하고자 한다. 수면 각성 제어의 수학적 모델링 1편과 2편에서 소개한 모델링 방법에 기초하여, 수면 모델링이 오늘날 어디까지 발전해있는지 볼 수 있는 기회가 되었으면 좋겠다.

최근 발표된 수면 모델들의 경우, 한 개의 수학 공식으로 수면 현상을 모두 설명하려고 하지 않는다. 수면과 각성 사이를 오가는 현상, 렘수면과 비렘수면 사이를 오가는 현상, 뇌에서 수면을 제어하는 신경들이 자극되는 정도, 신경전달물질들이 분비되는 패턴, 그리고 이 과정들에 영향을 줄 수 있는 내외 요인들을 각각 별개의 공식으로 설명하는 양상을 보인다. 그러므로 단일 “수학 공식”이라기보다는 “종합적인 개념적, 생리학적, 수학적 모델”을 만들어 수면과 관련된 다양한 현상과 상호작용을 풀어내려는 경향을 보인다.[1]

이제 개념적, 생리학적, 수학적 모델의 기본 틀을 이루는 요소들을 살펴보자.

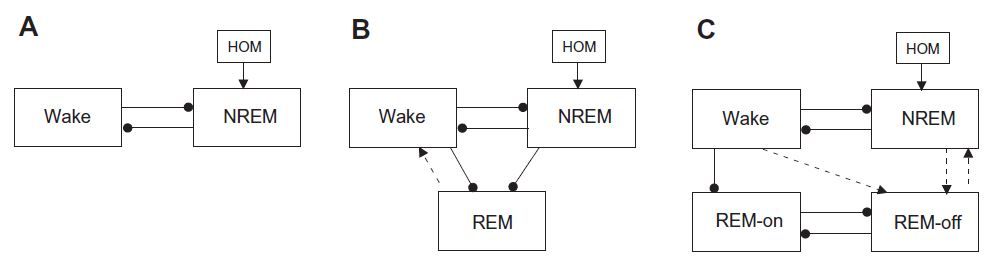
위 모식도는 수면 모델을 만들 때 고려하는 기본 틀로써 각성을 촉진하는 인자들, 수면을 촉진하는 인자들, 수면 중 렘수면을 촉진하는 인자들과 억제하는 인자들 등의 상호관계를 간단하게 표현하였다.[2] 성냥 모양의 선은 억제 작용을 하는 신경전달 과정을 의미하며, 화살표 모양은 촉진 과정을 뜻한다. 이 외에도 항상성 수면 욕구(homeostatic sleep drive, HOM)가 영향을 줄 수 있는 요소로 작용한다. 이 항상성 욕구의 한 예로 앞선 글(2편)에서 다루었던 생체리듬(circadian rhythm)을 들 수 있다.

그리고 이런 요소들 사이의 관계에, 앞선 글에서 언급했던 two-process model, sleep-wake flip-flop model, reciprocal interaction model, reciprocal inhibition model 등이 포괄적으로 응용되어 한 개의 모델을 생성하게 된다. Behn과 Booth의 모델을 예시로 살펴보자.

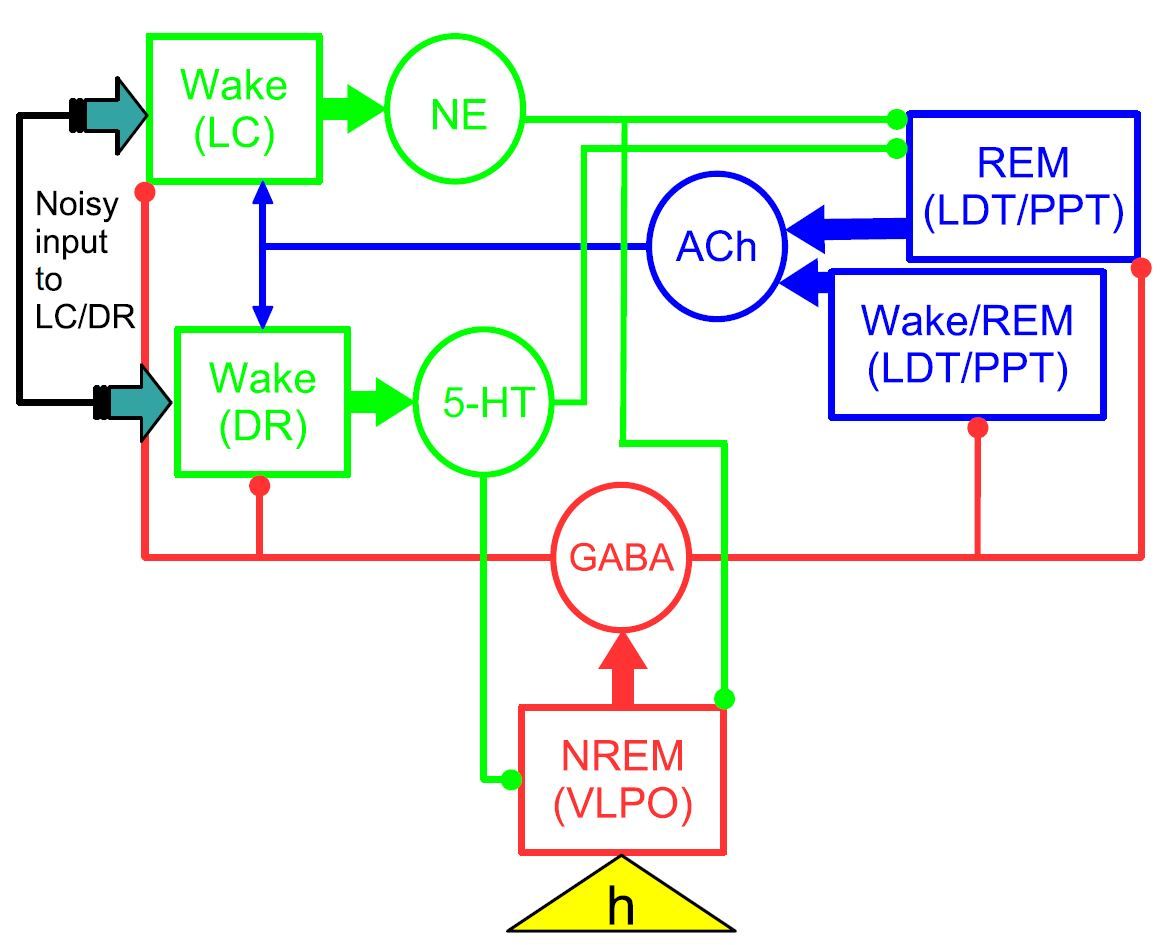
[그림 2]의 모식도는 언뜻 보면 복잡해보이지만 앞서 살펴보았던 수면-각성 조절과 관련된 sleep-wake flip-flop model과 렘수면 조절과 관련된 reciprocal interaction model 을 하나로 묶어서 수면 조절 과정을 하나의 모식도로 그린 것에 불과하다.[3] 이 그림에서 항상성 수면 욕구(homeostatic sleep drive)는 노란색 삼각형으로 표현하였고, 이것은 수면을 유도하는 ventrolateral preoptic nucleus(VLPO)에 작용을 한다. 뇌의 여러 부위 중 각성을 담당하는 부위는 초록색 사각형, 비렘수면을 유도하는 부위는 붉은색 사각형, 그리고 렘수면을 담당하는 부위는 푸른색 사각형으로 표시되어 있다. 각 부위가 수면과 각성, 그리고 렘수면에 어떻게 작용하는지는  1편과 2편에 상세히 설명하였으니 여기서는 생략하기로 한다.

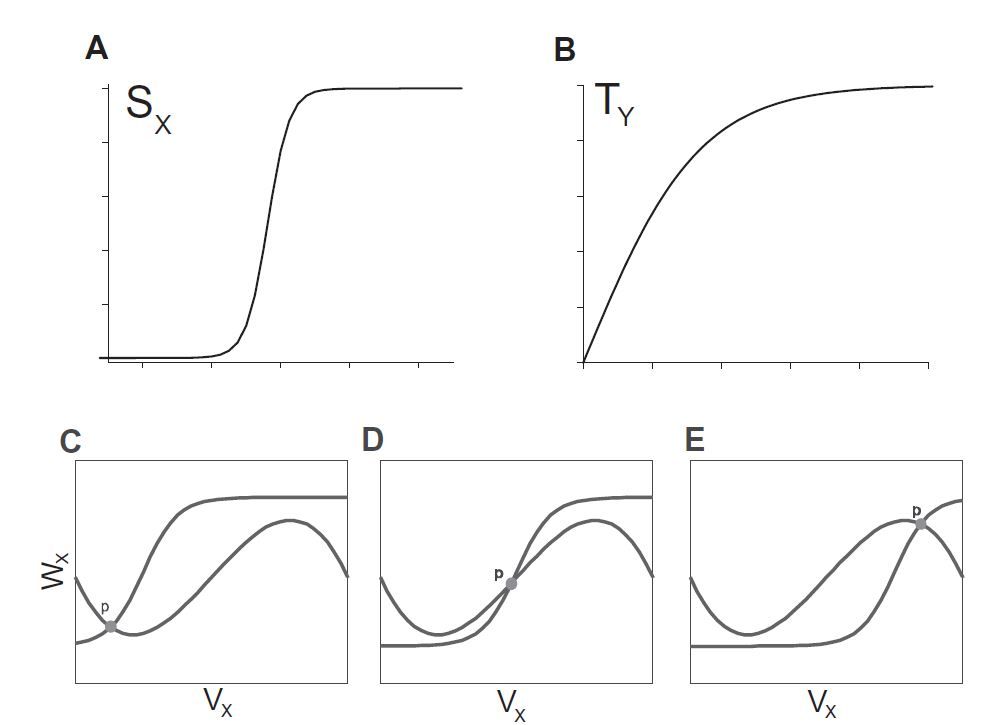
최근에 발표되고 있는 수학적 모델링은 결국 위와 같은 여러 신경핵들과 신경전달물질들의 작용을 수학적으로 풀어나가는 과정이다. 이 과정과 수학식이 간단하지 않은 이유는, 뇌에서 신경이 활성화되고, 신경전달물질이 쏟아져 나와, 다음 신경에 작용하기까지의 일련 과정이 어떻게 이루어지는지 정립된 이론이 없기 때문이다. 그림 3.에서 보듯이 실험적으로 측정된 신경 활성 빈도(neural firing rate)는 학자마다 S자형(sigmoid curve), 로그 함수형(saturating curve), 사인 곡선형(sinusoidal curve) 등 다양하게 해석하고 있기에 공식이 복잡해지기 마련이다.[2]

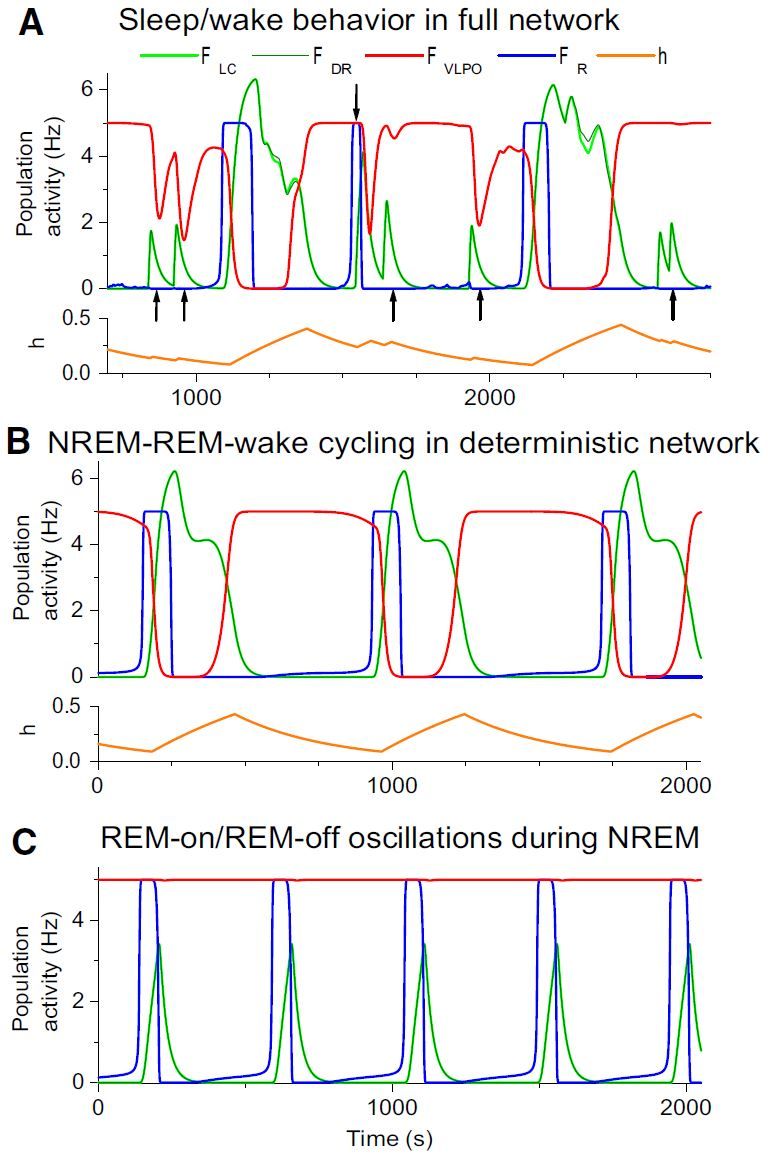
[그림4]에서 요약된 바와 같이 수면과 각성, 렘수면과 비렘수면을 조절하는 신경들이 활성화 되는 것은 수면 중 일정한 패턴을 가지고 반복된다.[3] 반복되는 이 싸이클을 가장 완벽하게 수학적으로 표현해내는 것이 궁극적인 수학적 모델링의 목표가 될 것이다.

이로써 총 세 편에 걸쳐 우리가 잠들고 깨는 현상과 꿈을 꾸는 렘수면이 주기적으로 반복되는 현상을 수학적으로 해석하여 표현하는 여러 이론들을 살펴보았다. 아직은 완벽하지 않은 여러 모델들이 정립되어가는 과정이기에 결정적인 역할을 하는 함수나 방정식을 이끌어내지는 못하였다. 그러나 실험적으로 측정되는 데이터가 충분히 축적된다면, 이 정보를 토대로 수학적으로 완벽하게 풀어낼 날이 곧 올 것이라 믿는다.

참고문헌

[1] R Gleit. Modeling interindividual differences in spontaneous internal desynchrony patterns. Journal of Biological Rhythms. 28 (2013) pp339-355.

[2] V Booth, C Behn. Physiologically-based modeling of sleep-wake regulatory networks. Mathematical Biosciences 250 (2014) pp54-68.

[3] C Behn, V Booth. Simulating microinjection experiments in a novel model of the rat sleep-wake regulatory network. Journal of Neurophysiology 103 (2010) pp1937-1953.

[그림 1,3]:  V Booth, C Behn. Physiologically-based modeling of sleep-wake regulatory networks. Mathematical Biosciences 250 (2014) pp54-68.

[그림 2,4] :C Behn, V Booth. Simulating microinjection experiments in a novel model of the rat sleep-wake regulatory network. Journal of Neurophysiology 103 (2010) pp1937-1953.